题目内容
在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
(1)当k=-2时,求反比例函数的解析式;
(2)已知经过原点O的两条直线AB与CD分别与双曲线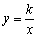 (k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
(k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
问:平行四边形ABCD能否成为矩形?能否成为正方形?若能,请说明直线AB、CD的位置关系;若不能,请说明理由
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(1)因为反比例函数的图象过点A(1,k),所以反比例函数的解析式是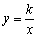 .
.
当k=-2时,反比例函数的解析式是 。
。
(2)当AB、CD关于直线y=x对称时,AB与CD互相平分且相等,ABCD是矩形.……(2分)
因为A、C可以无限接近坐标系但是不能落在坐标轴上,所以AB与CD无法垂直,因此四边形ABCD不能成为正方形.
(3)抛物线的顶点Q的坐标是 ,A、B关于原点O中心对称,
,A、B关于原点O中心对称,
当OQ=OA=OB时,△ABQ是以AB为直径的直角三角形.
由OQ2=OA2,得 .
.
解得 (如图2),
(如图2),

练习册系列答案
相关题目
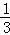 ,求AM的长.
,求AM的长.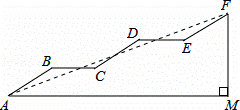
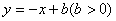 与双曲线
与双曲线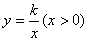 交于A,B两点,连接OA,OB,AM⊥y轴于M,AN⊥x轴于N,有以下结论: ①OA=OB; ②△AOM≌△BON;
交于A,B两点,连接OA,OB,AM⊥y轴于M,AN⊥x轴于N,有以下结论: ①OA=OB; ②△AOM≌△BON;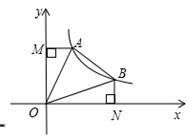
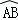 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则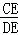 等于( )
等于( )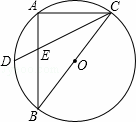
 )-1,b=
)-1,b= ,c=(2014-π)0,d=|1-
,c=(2014-π)0,d=|1- |,
|, , 3) D、(
, 3) D、( )
) ,那么这个角的补交的正弦值为 .
,那么这个角的补交的正弦值为 . 的根最接近( )
的根最接近( ) 中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。
中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。 DE
DE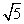 ,DE=2
,DE=2