题目内容
已知:如图1,在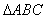 中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。
中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。
(1) 求∠AED的度数.
(2) ①求证:EB-EC= DE
DE
②若点A为直线AB上的动点,当点A运动到如图2位置时,①中的结论是否成立,若成立,说明理由;若不成立,直接写出类似的结论(不必证明)。
(3) 若点A运动到BD的延长线时,如图3所示,当DC=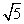 ,DE=2
,DE=2 时(0<BE<2),求AE的长。
时(0<BE<2),求AE的长。
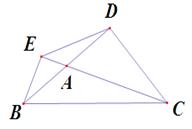
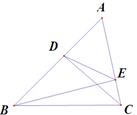
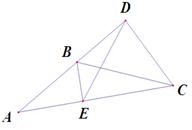
图1 图2 图3
(1)解:如图1:∵ CD⊥AB,BE⊥AC,垂足分别是D、E.
∴∠AEB=∠ADC=90°
∵∠A=∠A
∴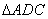 ∽
∽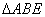
∴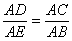
∴ 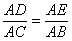
又∵∠A=∠A
∴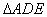 ∽
∽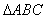
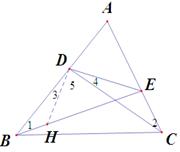
 ∴∠AED=∠ABC=45°
∴∠AED=∠ABC=45°
图1 图2
(2)①证明:如图2:在BE上截取BH=EC
∵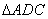 ∽
∽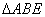
∴∠1=∠2
∵CD⊥AB
∴∠BDC=90°且∠ABC=45°
∴BD=DC
在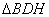 和
和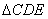 中
中
 ∵ BD=DC,∠1=∠2 ,BH=EC
∵ BD=DC,∠1=∠2 ,BH=EC
∴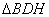 ≌
≌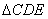 (SAS)
(SAS)
∴DH=DE ∠3=∠4
∵∠3+∠5=90°
∴∠HDE=∠4+∠5=90°
∴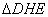 为等腰直角三角形
为等腰直角三角形
∴BE-EC=BE-BH=HE= DE
DE
∴BE - EC= DE
DE
②如图2,原结论不成立,,结论应为:EC-BE= DE
DE
(3)如图3:延长EB到H,使BH=EC
同理可证: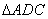 ∽
∽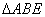 ,
,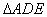 ∽
∽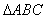
∠DEC=45° ∴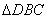 为等腰直角三角形
为等腰直角三角形
∵∠1=∠2=∠DCE
BD=DC
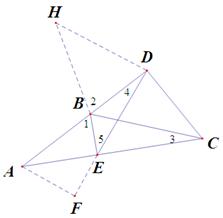 BH=EC
BH=EC
∴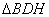 ≌
≌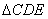 (SAS)
(SAS)
∴DE=DH
∴∠5=180°-90°-45°=45°
∴∠5=∠H=45°
∴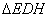 为等腰直角三角形
为等腰直角三角形
∴HB+BE=EC+BE=HB= DE 图3
DE 图3
∴EC+BE= DE
DE
设BE=x
∵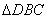 为等腰直角三角形
为等腰直角三角形
∴BC= DC=
DC=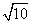
∵EC+BE= DE 即EC+X=
DE 即EC+X= ·
·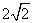 =4
=4
∴EC=4-X
在Rt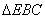 中,由勾股定理得:
中,由勾股定理得:
解得:X=1或3
∵ 0<BE<2
∴ BE=1 (如图3)
∴tan∠3=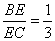
延长DE,过点A作AF⊥DE的延长线于点F
在Rt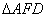 中,tan∠4= tan∠3=
中,tan∠4= tan∠3=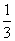
∵∠AEF=∠DEC=45°
∴设AF=EF=a 则DF=3a
∴ DE=3a-a=2a=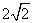
∴ a=
∴AE= ·
· =2
=2

某班级学生参加初三体育考试,其中有20名同学参加了排球发球考试,裁判将发球过网个数记入下表,由于不小心弄脏了表格,有两个数据看不到. 则下列说法中正确的是( )
| 过网个数 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 5 |
A.这组数据众数是8 B.这组数据的中位数是7.5
C.这组数据的方差是4 D.这组数据的平均数P满足8.1<P<8.6
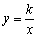 (k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
(k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形. (2)解方程:
(2)解方程:



 的倒数是 ( )
的倒数是 ( ) C、4 D、-4
C、4 D、-4