题目内容
14. 如图,已知线段AD和BC的公共部分CD=$\frac{1}{3}$AC=$\frac{1}{2}$BC,线段AC的中点为E,若DE=10cm,求AC,BC的长.
如图,已知线段AD和BC的公共部分CD=$\frac{1}{3}$AC=$\frac{1}{2}$BC,线段AC的中点为E,若DE=10cm,求AC,BC的长.
分析 先根据设CD=x,根据CD=$\frac{1}{3}$AC=$\frac{1}{2}$BC,得出AC=3x,BC=2x,CE=1.5x,再根据DE=10cm,列出方程求解即可得到x的值,最后计算AC,BC的长.
解答 解:设CD=x,则AC=3x,BC=2x,
∵线段AC的中点为E,
∴CE=1.5x,
∵DE=10cm,
∴CE+CD=10cm,
即1.5x+x=10,
解得x=4,
∴AC=3x=12cm,BC=2x=8cm.
点评 本题主要考查了两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键,解题时注意方程思想的运用.

练习册系列答案
相关题目
5.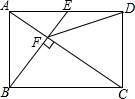 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
12.下列计算正确的是( )
| A. | 2a2•4ab2=6a3b2 | B. | 3a3•4a4=7a12 | C. | 3x2•2x5=6a10 | D. | 0.1x•10x2=x3 |