题目内容
 如图,在⊙O中,弦AB所对的优弧为圆的
如图,在⊙O中,弦AB所对的优弧为圆的| 2 |
| 3 |
考点:垂径定理,勾股定理,圆心角、弧、弦的关系
专题:
分析:根据已知先求得∠AOB=120°,进而求得∠A=∠B=30°,作OC⊥AB于C,解直角三角形求得AC,即可求得AB.
解答: 解:∵弦AB所对的优弧为圆的
解:∵弦AB所对的优弧为圆的
,
∴∠AOB=120°,
∴∠A=∠B=30°,
作OC⊥AB于C,
∴AC=BC,
∴AC=cosA•OA=
×4=2
,
∴AB=2AC=4
.
 解:∵弦AB所对的优弧为圆的
解:∵弦AB所对的优弧为圆的| 2 |
| 3 |
∴∠AOB=120°,
∴∠A=∠B=30°,
作OC⊥AB于C,
∴AC=BC,
∴AC=cosA•OA=
| ||
| 2 |
| 3 |
∴AB=2AC=4
| 3 |
点评:本题考查了垂径定理,圆心角、弧、弦的关系,解直角三角形等,作出辅助线构建直角三角形是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
计算:(6ab2-4a2b)•3ab的结果是( )
| A、18a2b3-12a3b2 |
| B、18ab3-12a3b2 |
| C、18a2b3-12a2b2 |
| D、18a2b2-12a3b2 |
平行四边形的一条边长是10cm,那么它的两条对角线的长可能是( )
| A、6cm和8cm |
| B、10cm和20cm |
| C、8cm和12cm |
| D、12cm和32cm |
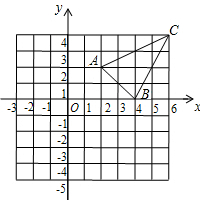 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为 如图所示,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立平面直角坐标系,回答下列问题:
如图所示,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立平面直角坐标系,回答下列问题: 如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.
如图,四边形ABCD中,∠A=90°,∠C=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系. 在直角坐标系中直接画出函数y=|x|的图象.若一次函数y=kx+b的图象分别过点A(-1,1)、B(2,2),请你依据这两个函数的图象写出方程组
在直角坐标系中直接画出函数y=|x|的图象.若一次函数y=kx+b的图象分别过点A(-1,1)、B(2,2),请你依据这两个函数的图象写出方程组 如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是
如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是