题目内容
 如图,在△ABC和△ADE中,B,D,E,C在同一条直线上,下面给出三个条件:
如图,在△ABC和△ADE中,B,D,E,C在同一条直线上,下面给出三个条件:①AB=AC;②AD=AE;③BD=EC,请你选两个作为已知条件,余下一个作为结论,要求得到一个真命题,先完成填空,再证明.
你选择的条件:
考点:等腰三角形的性质,命题与定理
专题:
分析:由已知题设①AB=AC,②AD=AE,则得∠B=∠C,∠ADE=∠AED,所以得:∠ADB=∠AEC,即得△ABD≌△ACE,从而证得③BD=CE.
解答:条件:①②,结论③.
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
在△ABD和△ACE中,
∵
,
∴△ABD≌△ACE(AAS),
∴BD=CE.
故答案为:①②,③.
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
在△ABD和△ACE中,
∵
|
∴△ABD≌△ACE(AAS),
∴BD=CE.
故答案为:①②,③.
点评:本题考查的是等腰三角形的性质,熟知等腰三角形的两底角相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
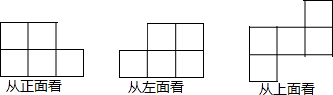 如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )
如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )| A、8个 | B、7个 | C、6个 | D、5个 |
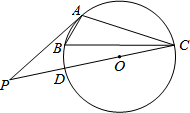 如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.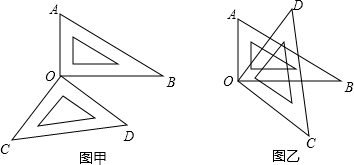
 如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是
如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是
 如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为2
如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为2 某学校开展数学竞赛,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班的5名选手的复赛成绩如图所示.根据图示回答:一班复赛成绩的中位数是
某学校开展数学竞赛,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班的5名选手的复赛成绩如图所示.根据图示回答:一班复赛成绩的中位数是