题目内容
19.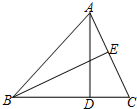 如图,AD、BE分别是△ABC中BC、AC边上的高,AD=4,AC=6,则sin∠EBC=$\frac{\sqrt{5}}{3}$.
如图,AD、BE分别是△ABC中BC、AC边上的高,AD=4,AC=6,则sin∠EBC=$\frac{\sqrt{5}}{3}$.
分析 根据AD、BE分别是△ABC中BC、AC边上的高,可以求得∠EBC和∠DAC的关系,AD=4,AC=6,可以求得CD的长,从而可以求出∠DAC的三角函数值,进而可以得到∠EBC的三角函数值,本题得以解决.
解答 解:∵AD、BE分别是△ABC中BC、AC边上的高,
∴∠BDA=∠ADC=90°,
∴∠CBE=∠DAC,
∵∠ADC=90°,AD=4,AC=6,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}=\sqrt{{6}^{2}-{4}^{2}}=\sqrt{20}=2\sqrt{5}$,
∴sin$∠DAC=\frac{CD}{AC}=\frac{2\sqrt{5}}{6}=\frac{\sqrt{5}}{3}$,
∴sin∠EBC=$\frac{\sqrt{5}}{3}$,
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查解直角三角形,解题的关键找出各个角之间的关系,利用等角的三角函数值相等,可以求得所求的角的三角函数值.

练习册系列答案
相关题目
8.下列各组代数式中,是同类项的是( )
| A. | 3ab2,$\frac{1}{3}$a2b | B. | 2x3y2,-y2x3 | C. | 5ab,$\frac{1}{5}$abc | D. | -3a3y2,2a2b2 |
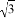 是指坡面的铅直高度BC与水平宽度AC的比,若堤高BC=5m,则坡面AB的长度是( )
是指坡面的铅直高度BC与水平宽度AC的比,若堤高BC=5m,则坡面AB的长度是( )