题目内容
已知△ABC的角平分线BM、CN相交于点P，求证：AP平分∠BAC．
考点：角平分线的性质
专题：证明题
分析：过P作P⊥AB于M，PN⊥AC于N，PH⊥BC于H，根据角平分线性质求出PM=PH，PH=PN，推出PM=PN，根据角平分线性质得出即可．
解答：证明：
过P作P⊥AB于M，PN⊥AC于N，PH⊥BC于H，
∵△ABC的角平分线BM、CN相交于点P，
∴PM=PH，PH=PN，
∴PM=PN，
∵PM⊥AB，PN⊥AC，
∴AP平分∠BAC．
过P作P⊥AB于M，PN⊥AC于N，PH⊥BC于H，
∵△ABC的角平分线BM、CN相交于点P，
∴PM=PH，PH=PN，
∴PM=PN，
∵PM⊥AB，PN⊥AC，
∴AP平分∠BAC．
点评：本题考查了角平分线的性质的应用，注意：角平分线上的点到这个角的两边的距离相等．
练习册系列答案
相关题目
下列各式中，代数式的个数有（ ）
①a；②ab=ba；③0；④2x=6；⑤mx-ny；⑥
；⑦m2-
．
①a；②ab=ba；③0；④2x=6；⑤mx-ny；⑥
| a |
| b |
| 1 |
| n |
| A、2个 | B、3个 | C、4个 | D、5个 |
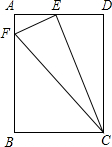已知：如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连接FC．（AB＞AE）
阅读并完成下列的计算过程：