题目内容
3.现有若干张如图1所示的正方形纸片A,B和长方形纸片C.(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:a2+2ab+b2=(a+b)2;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是2,并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
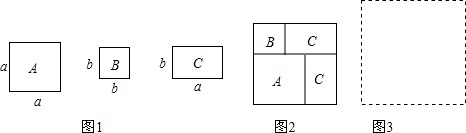
分析 (1)利用面积相等易得a2+2ab+b2=(a+b)2;
(2)由于有a2+3ab,则a2+3ab+nb2分解为(a+b)(a+2b),因此得到n=2,再画图;
(3)利用面积可分解因式.
解答 解:(1)利用面积相等得a2+2ab+b2=(a+b)2;
(2)由于有a2+3ab,则a2+3ab+nb2分解为(a+b)(a+2b),因此得到n=2,
如图: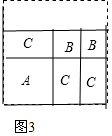
(3)a2+5ab+4b2=(a+b)(a+4b).
故答案为a2+2ab+b2=(a+b)2;2;a2+5ab+4b2=(a+b)(a+4b).
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | xm+xm=x2m | B. | x3•x3=x6 | C. | 2-2=-4 | D. | x6÷x2=x3 |
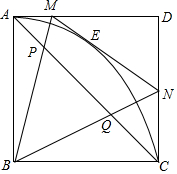 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.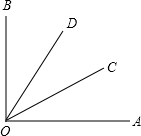 如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.