题目内容
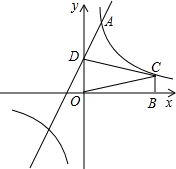
 如图,在平面直角坐标中,四边形OABC是正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A(0,8),则经过圆心M的反比例函数的解析式为.
如图,在平面直角坐标中,四边形OABC是正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A(0,8),则经过圆心M的反比例函数的解析式为.考点:切线的性质,反比例函数图象上点的坐标特征,正方形的性质
专题:
分析:过点M作MD⊥AB于D,连接AM,设⊙M的半径为R,因为四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,若点A的坐标为(0,8),所以DA=4,AB=8,DM=8-R,AM=R,又因△ADM是直角三角形,利用勾股定理即可得到关于R的方程,解之即可得到M的坐标,进而求出经过圆心M的反比例函数的解析式
解答:解:过点M作MD⊥AB于D,连接AM,设⊙M的半径为R,
∵四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,点A的坐标为(0,8),
∴DA=4,AB=8,DM=8-R,AM=R,
又∵△ADM是直角三角形,
根据勾股定理可得AM2=DM2+AD2,
∴R2=(8-R)2+42,
解得R=5,
∴M(-4,5).
∴经过圆心M的反比例函数的解析式为y=
=-
.
∵四边形OABC为正方形,顶点A,C在坐标轴上,以边AB为弦的⊙M与x轴相切,点A的坐标为(0,8),

∴DA=4,AB=8,DM=8-R,AM=R,
又∵△ADM是直角三角形,
根据勾股定理可得AM2=DM2+AD2,
∴R2=(8-R)2+42,
解得R=5,
∴M(-4,5).
∴经过圆心M的反比例函数的解析式为y=
| -4×5 |
| x |
| 20 |
| x |
点评:本题主要考查了垂径定理,正方形的性质、勾股定理的运用以及运用待定系数法求比例系数.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,已知平面直角坐标系xOy中,直线y=k1x+2与反比例函数
如图,已知平面直角坐标系xOy中,直线y=k1x+2与反比例函数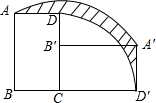 如图,矩形ABCD中,AB=8,BC=6,现将此矩形绕点C顺时针旋转90°得到新的矩形A′B′CD′,则边AD扫过的面积(阴影部分)是
如图,矩形ABCD中,AB=8,BC=6,现将此矩形绕点C顺时针旋转90°得到新的矩形A′B′CD′,则边AD扫过的面积(阴影部分)是 甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数 字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数 时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘,则甲获胜的概率是( )
甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数 字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数 时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘,则甲获胜的概率是( )