题目内容
1．
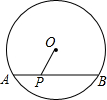如图，在⊙O中，弦AB的长为8，圆心O到AB的距离为3．（1）求⊙O的半径；
（2）若点P是AB上的一动点，试求线段OP的取值范围．
分析 （1）作OC⊥AB于点C，构造直角三角形，利用勾股定理求得半径即可；
（2）最长等于半径，最小等于弦心距．
解答 
解：（1）作OC⊥AB于点C，
∵圆心O到AB的距离为3，
∴OC=3，
∵弦AB的长为8，
∴AC=BC=4，
∴OA=$\sqrt{O{C}^{2}+A{C}^{2}}$=5，
∴⊙O的半径为5；
（2）∵点P是AB上的一动点，
∴3≤PO≤5．
点评 本题考查了垂径定理的知识，平分弦的直径平分这条弦，并且平分弦所对的两条弧，需要同学们熟练掌握．
练习册系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
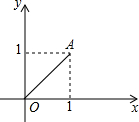如图，点A的坐标是（1，1），如果将线段OA绕点O按逆时针方向旋转135°，那么点A旋转后的对应点的坐标是（$-\sqrt{2}$，0）．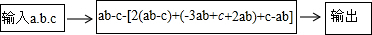
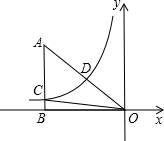如图，已知双曲线y=$\frac{k}{x}$（k＜0）经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C．已知点A的坐标为（-6，4）．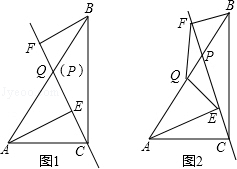
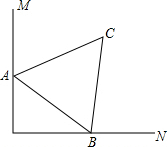如图，∠MON=90°，已知△ABC，AC=BC=5，AB=6，三角形ABC的顶点A、B分别在边OM，ON上当B在边ON上运动时，A随之在边OM上运动，三角形ABC的形状保持不变，在运动过程中，点C到点O的最大距离为7．
如图，OA、OB是⊙O的半径，∠OAB=45°，AO=5，则AB=5$\sqrt{2}$．