题目内容
9.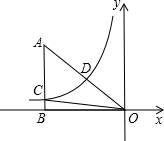 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.已知点A的坐标为(-6,4).
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.已知点A的坐标为(-6,4).(1)求此反比例函数的解析式;
(2)连接OC,求△AOC的面积.
分析 (1)把点D的坐标代入反比例函数解析式来求k的值;
(2)由反比例函数解析式可以求得点C的坐标为(-6,1),则由点的坐标与图形的性质和三角形的面积公式进行解答即可.
解答 解:(1)∵点D是Rt△OAB斜边OA的中点,点A的坐标为(-6,4),
∴D(-3,2),
把(-3,2)代入y=$\frac{k}{x}$(k<0),得到
k=xy=(-3)×2=-6,
故该反比例函数解析式为:y=-$\frac{6}{x}$;
(2)∵由(1)知,反比例函数解析式为:y=-$\frac{6}{x}$,且C(-6,1),
∴S△AOC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×3×6=9.
点评 本题考查了反比例函数图象上点的坐标特征和待定系数法求反比例函数解析式,熟知反比例函数中k=xy的特点是解答此题的关键.

练习册系列答案
相关题目
19.近似数8.01×104精确到( )
| A. | 万位 | B. | 百分位 | C. | 万分位 | D. | 百位 |
4.近似数5.83×105是精确到( )
| A. | 百位 | B. | 千位 | C. | 百分位 | D. | 千分位 |
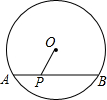 如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.
如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.