题目内容
5.已知m,n为两个连续的整数,且m<6-$\sqrt{11}$<n,则m+n=5.分析 先估算出$\sqrt{11}$的大小,然后再利用不等式的性质求得m、n的值,最后代入计算即可.
解答 解:∵9<11<16,
∴3<$\sqrt{11}$<4.
∴-3>-$\sqrt{11}$>-4,
∴6-3>6-$\sqrt{11}$>6-4,即3>6-$\sqrt{11}$>2.
∴m=2,n=3,
∴m+n=2+3=5.
故答案为:5.
点评 本题主要考查的是估算无理数的大小,掌握估算无理数大小的方法是解题的关键.

练习册系列答案
相关题目
5.下列等式不成立的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$ |
20.在下列多项式乘法运算中,不能运用平方差公式进行运算的是( )
| A. | (2x+3y)(-2x+3y) | B. | (a-2b)(a+2b) | C. | (-x-2y)(x+2y) | D. | (-2x-3y)(3y-2x) |
14.如图,BF、CF分别是∠DBC和∠ECB的角平分线,则关于F的说法不正确的是( )
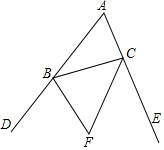

| A. | F到△ABC三边所在直线的距离相等 | B. | F在∠A的平分线上 | ||
| C. | F到△ABC三顶点的距离相等 | D. | F到BD、CE的距离相等 |
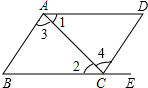 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B+∠BAD=180°;④AD∥BE且∠D=∠B.其中,能推出AB∥DC的条件为②④.(填写序号)
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B+∠BAD=180°;④AD∥BE且∠D=∠B.其中,能推出AB∥DC的条件为②④.(填写序号)