题目内容
2.阅读下列材料:1×2=$\frac{1}{3}$(1×2×3-0×1×2),
2×3=$\frac{1}{3}$(2×3×4-1×2×3),
3×4=$\frac{1}{3}$(3×4×5-2×3×4),
由以上三个等式相加,可得:1×2+2×3+3×4=$\frac{1}{3}×$3×4×5=20.
根据以上材料,请你完成下列各题:
(1)1×2+2×3+3×4+…+10×11;(写出过程)
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2);
(3)根据以上学习经验,猜想1×2×3+2×3×4+…+8×9×10=3960.
分析 (1)利用已知材料得出原式=$\frac{1}{3}$×10×11×12,进而求出即可;
(2)利用(1)中所求,进而求出即可;
(3)仿照已知得出原式=$\frac{1}{4}$(1×2×3×4)+$\frac{1}{4}$(2×3×4×5-1×2×3×4)+$\frac{1}{4}$(3×4×5×6-2×3×4×5)+…+$\frac{1}{4}$(9×10×11×12-8×9×10×11)进而求出即可.
解答 解:(1)1×2+2×3+3×4+…+10×11
=$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+$\frac{1}{3}$(3×4×5-2×3×4)+…+$\frac{1}{3}$(10×11×12-9×10×11)
=$\frac{1}{3}$(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+10×11×12-9×10×11)
=$\frac{1}{3}$×10×11×12
=440;
(2)1×2+2×3+3×4+…+n(n+1)
=$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+$\frac{1}{3}$(3×4×5-2×3×4)+…+$\frac{1}{3}$[n×(n+1)×(n+2)-(n-1)×n×(n+1)]
=$\frac{1}{3}$n(n+1)(n+2);
(3)1×2×3+2×3×4+3×4×5+…+10×11×12
=$\frac{1}{4}$(1×2×3×4)+$\frac{1}{4}$(2×3×4×5-1×2×3×4)+$\frac{1}{4}$(3×4×5×6-2×3×4×5)+…+$\frac{1}{4}$(9×10×11×12-8×9×10×11)
=$\frac{1}{4}$×9×10×11×12
=3960.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用找出的规律解决问题.

 阅读快车系列答案
阅读快车系列答案
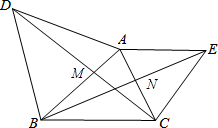 如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证:
如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证: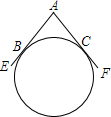 一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.
一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.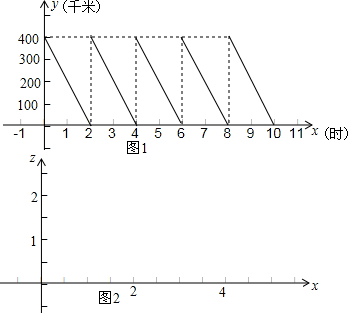 我们已经研究过函数的增减性(即单调性)、函数的对称性(即奇偶性)、函数的有界性,今天我们来研究一下函数的周期性.生活中有很多具有周期性的例子,如钟表的指针绕钟表圆心周而复始的旋转等,再如下面的例子:
我们已经研究过函数的增减性(即单调性)、函数的对称性(即奇偶性)、函数的有界性,今天我们来研究一下函数的周期性.生活中有很多具有周期性的例子,如钟表的指针绕钟表圆心周而复始的旋转等,再如下面的例子: