题目内容
14.(1)已知线段AB=8,点C在线段AB的延长线上,M、N分别是线段AC与线段BC的中点,求线段MN的长;(2)已知线段AB=8cm,点C在线段AB的反向延长线上,M、N分别是线段AC与线段BC的中点,则线段MN的长为4cm.
分析 (1)根据M为AC的中点,N为BC的中点,于是得到CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,然后根据线段和差即可得到结论;
(2)根据M为AC的中点,N为BC的中点,于是得到CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,然后根据线段和差即可得到结论.
解答 解:(1)如图1,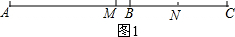
∵M为AC的中点,N为BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CM-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB=4.
(2)如图2,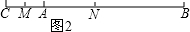
∵M为AC的中点,N为BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CN-CM=$\frac{1}{2}$BC-$\frac{1}{2}$AC=$\frac{1}{2}$(BC-AC)=$\frac{1}{2}$AB=4.
故答案为:4.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
15.$\frac{3}{2}$的倒数是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{3}{2}$ |
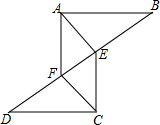 如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.