题目内容
7.已知二次函数y1=mx2-2mx-3(m>0)与一次函数y2=x+1,令W=y1-y2.(1)若y1、y2的函数图象交于x轴上的同一点.
①求m的值;
②当x为何值时,W的值最小,试求出该最小值;
(2)当-2<x<3时,W随x的增大而减小.
①求m的取值范围;
②求证:y1<y2.
分析 (1)①直接得出一次函数y2=x+1过(-1,0),进而代入二次函数解析式得出答案;
②直接利用m的值得出W与x的函数关系式,进而得出最值;
(2)①首先表示出二次函数的对称轴,进而二次函数增减性得出m的取值范围;
②首先得出当x=-2时,W的值,进而得出W<W0≤0,即y1-y2<0,即可得出答案.
解答 解:(1)①∵y1、y2的函数图象交于x轴上的同一点,一次函数y2=x+1过(-1,0),
∴二次函数y1=mx2-2mx-3(m>0)过(-1,0),
∴0=m+2m-3,
解得:m=1;
②W=x2-2x-3-x-1=x2-3x-4=(x-$\frac{3}{2}$)2-$\frac{25}{4}$,
当x=$\frac{3}{2}$时,W的值最小,最小值为:-$\frac{25}{4}$;
(2)①解:W=mx2-2mx-3-x-1=mx2-(2m+1)x-4,
对称轴为:x=-$\frac{-(2m+1)}{2m}$=$\frac{2m+1}{2m}$,
因为m>0,-2<x<3时,且W随x的增大而减小,
所以,$\frac{2m+1}{2m}$≥3,
所以m≤$\frac{1}{4}$,
所以0<m≤$\frac{1}{4}$,
②证明:当x=-2时,W0=y1-y2=8m-2,
因为-2<x<3时,W随x的增大而减小.
所以,W<W0=8m-2,
因为0<m≤$\frac{1}{4}$,所以8m-2≤0,即W0≤0,
所以W<W0≤0,即y1-y2<0,
所以y1<y2.
点评 此题主要考查了二次函数综合以及二次函数的性质等知识,正确利用二次函数的性质分析是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.剪纸,又叫刻纸,是一种镂空艺术,是中国汉族最古老的民间艺术之一,它在视觉上给人以透空的感觉和艺术享受,它较多地利用了图形的轴对称的性质,以下几个剪纸图案是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.如图,∠1和∠2是对顶角的图形是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.
如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.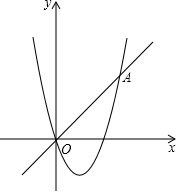 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.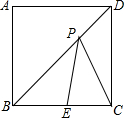 在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到$\sqrt{13}$.
在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到$\sqrt{13}$.