题目内容
20.解不等式组.(1)$\left\{\begin{array}{l}{3(1-x)<2(x+9)}\\{\frac{x-3}{0.5}-\frac{x+4}{0.2}≤-14}\end{array}\right.$;
(2)2x<1-x≤x+5.
分析 (1)先求出每个不等式的解集,再求出不等式组的解集即可.
(2)原式可转化为一个不等式组,先求出两个不等式的解集,再求其公共解.
解答 解:(1)$\left\{\begin{array}{l}{3(1-x)<2(x+9)①}\\{\frac{x-3}{0.5}-\frac{x+4}{0.2}≤-14②}\end{array}\right.$
∵由①得:x>-3,
由②得:x≥-4,
∴原不等式组的解集为x>-3.
(2)将不等式组:2x<1-x≤x+5.化为:$\left\{\begin{array}{l}{2x<1-x①}\\{1-x≤x+5②}\end{array}\right.$
由(1)得x<$\frac{1}{3}$,
由(2)得x≥-2,
所以不等式组的解集为-2≤x<$\frac{1}{3}$.
点评 本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集.

练习册系列答案
相关题目
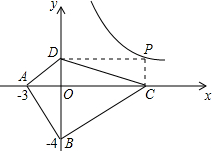 如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.
如图,已知A(-3,0),B(0,-4),P为双曲线y=$\frac{12}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则四边形ABCD面积的最小值为24.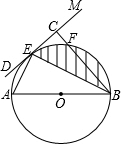 如图所示,已知⊙O的直径AB=8cm,BE为⊙O的弦,直接DM经过点E,且∠MEB=∠A作BC⊥DM于点C,BC交⊙O于点F,BC=6cm
如图所示,已知⊙O的直径AB=8cm,BE为⊙O的弦,直接DM经过点E,且∠MEB=∠A作BC⊥DM于点C,BC交⊙O于点F,BC=6cm