题目内容
6.如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;
(2)猜想线段AD、BE、DE之间的关系,并说明理由.
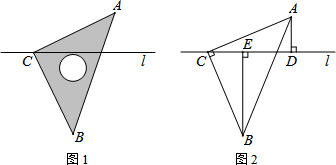
分析 (1)观察图形,结合已知条件,可知全等三角形为:△ACD与△CBE.根据AAS即可证明;
(2)由(1)知△ACD≌△CBE,根据全等三角形的对应边相等,得出CD=BE,AD=CE,从而求出线段AD、BE、DE之间的关系.
解答 证明:(1)∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB.
在△ACD与△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS);
(2)AD=BE-DE,理由如下:
∵△ACD≌△CBE,
∴CD=BE,AD=CE,
又∵CE=CD-DE,
∴AD=BE-DE
点评 本题考查全等三角形的判定与性质,余角的性质,关键是根据AAS证明三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.嘉峪关市约有20.5万人,把近似数205000用科学记数法表示为( )
| A. | 205×103 | B. | 20.5×104 | C. | 2.05×105 | D. | 0.205×106 |
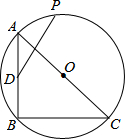 如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$.
如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$. 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:∠ABE=∠ACE.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:∠ABE=∠ACE.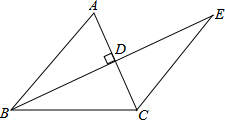 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.