题目内容
17．下面的多项式中，能因式分解的是（ ）| A． | m2+n2 | B． | m2+4m+1 | C． | m2-n | D． | m2-2m+1 |
分析 根据因式分解是把一个多项式化成几个整式乘积的形式，可得答案．
解答 解：m2-2m+1=（m-1）2，
故选：D．
点评 本题考查了因式分解的意义，因式分解是把一个多项式化成几个整式乘积的形式，因式分解的方法是一提取公因式，二套用公式，三分解要彻底．
练习册系列答案
相关题目
2．某校要从四名学生中选拔一名参加市“风华小主播”大赛，选拔赛中每名学生的平均成绩$\overline{x}$及其方差s2如表所示，如果要选择一名成绩高且发挥稳定的学生参赛，则应选择的学生是（ ）
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8 | 9 | 9 | 8 |
| s2 | 1 | 1 | 1.2 | 1.3 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
8．在?ABCD中，对角线AC和BD相交于点O，如果AC=24，BD=20，AB=m，则m的取值范围是（ ）
| A． | 20＜m＜24 | B． | 4＜m＜44 | C． | 2＜m＜22 | D． | 10＜m＜12 |
5．下列分式一定有意义的是（ ）
| A． | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B． | $\frac{x+1}{{x}^{2}}$ | C． | $\frac{x-1}{{x}^{2}+1}$ | D． | $\frac{{x}^{2}}{x+1}$ |
12．三角形三边长为6、8、10，那么最长边上的高为（ ）
| A． | 6 | B． | 4.5 | C． | 4.8 | D． | 8 |
2．
已知OA，OB是⊙O的半径，点C在⊙O上，∠OBA=50°，则∠C的度数为（ ）
已知OA，OB是⊙O的半径，点C在⊙O上，∠OBA=50°，则∠C的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 80° |
9．已知a=2-$\sqrt{3}$，b=$\sqrt{3}+2$，则a、b的关系为（ ）
| A． | 相等 | B． | 互为相反数 | C． | 互为倒数 | D． | 互为负倒数 |
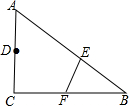如图，在△ABC中，∠C=90°，AC=6，BC=9，将△ABC沿EF翻折点B恰好落在CA的中点D处，则折痕EF的长为$\sqrt{10}$．