题目内容
2.五个正方形按如图放置在直线l上,其中第1、2、4个正方形的面积分别为2、5、4,则第5个正方形的面积S5=1.
分析 由AAS证明△ABC≌△CDE,得出AB=CD,同理:△FGH≌△HMN,得出FG=HM=$\sqrt{N{H}^{2}-M{N}^{2}}$=$\sqrt{5-2}$=$\sqrt{3}$,得出DE,由勾股定理求出CD,得出AB,即可得出结果.
解答 解:如图所示:
由正方形的性质得:∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
在△ABC和△EDC中,$\left\{\begin{array}{l}{∠1=∠3}&{\;}\\{∠ABC=∠CDE=90°}&{\;}\\{AC=CE}&{\;}\end{array}\right.$,
∴△ABC≌△CDE(AAS),
∴AB=CD,
同理:△FGH≌△HMN,
∴FG=HM=$\sqrt{N{H}^{2}-M{N}^{2}}$=$\sqrt{5-2}$=$\sqrt{3}$,
∴DE=FG=$\sqrt{3}$,
∴CD=$\sqrt{C{E}^{2}-D{E}^{2}}$=$\sqrt{4-3}$=1,
∴AB=1,
∴S5=AB2=1;
故答案为:1.
点评 本题考查了正方形的性质、勾股定理、全等三角形的判定与性质;熟练掌握勾股定理,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 两个长度相等的弧是等弧 | ||
| C. | 相等的圆心角所对的弧相等 | D. | 90°的圆周角所对的弦是直径 |
17.下列计算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-4)^{2}}$=-4 | C. | $±\sqrt{8}=±4$ | D. | (-$\sqrt{2}$)2=2 |
 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,且AE=DE.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,且AE=DE.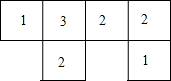 如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.
如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.