题目内容
 如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.
考点:扇形面积的计算,等腰梯形的判定
专题:
分析:(1)根据题意得出AB=CD且∠CAD=∠ACB=30°,进而得出BC∥AD,即可得出答案;
(2)利用S阴影=S扇形BOD-S△BOD,进而求出即可.
(2)利用S阴影=S扇形BOD-S△BOD,进而求出即可.
解答: (1)证明:∵∠BAD=120°,AB=AD,
(1)证明:∵∠BAD=120°,AB=AD,
∴∠ABD=∠ADB=30°,
∴弧AB和弧AD的度数都等于60°,
又∵BC是直径,
∴弧CD的度数也是60°,
∴AB=CD且∠CAD=∠ACB=30°,
∴BC∥AD,
∴四边形ABCD是等腰梯形;
(2)解:∵BC是直径,
∴∠BAC=90°
∵∠ACB=30°,AC=6,
∴BC=
=
=4
,故R=2
,
∵弧AB和弧AD的度数都等于60°,
∴∠BOD=120°,
连接OA交BD于点E,则OA⊥BD,
在Rt△BOE中:OE=OBsin30°=
,BE=OB•cos30°=3,BD=2BE=6,
故S阴影=S扇形BOD-S△BOD=
-
×6×
=4π-3
.
 (1)证明:∵∠BAD=120°,AB=AD,
(1)证明:∵∠BAD=120°,AB=AD,∴∠ABD=∠ADB=30°,
∴弧AB和弧AD的度数都等于60°,
又∵BC是直径,
∴弧CD的度数也是60°,
∴AB=CD且∠CAD=∠ACB=30°,
∴BC∥AD,
∴四边形ABCD是等腰梯形;
(2)解:∵BC是直径,
∴∠BAC=90°
∵∠ACB=30°,AC=6,
∴BC=
| AC |
| cos30° |
| 6 | ||||
|
| 3 |
| 3 |
∵弧AB和弧AD的度数都等于60°,
∴∠BOD=120°,
连接OA交BD于点E,则OA⊥BD,
在Rt△BOE中:OE=OBsin30°=
| 3 |
故S阴影=S扇形BOD-S△BOD=
120×π×(2
| ||
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查了扇形面积求法以及等腰梯形的判定等知识,得出半径长是解题关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在下列各数中是有理数的有( )
A、
| ||
B、
| ||
| C、π | ||
| D、2.010010001… |
下列二次根式中,是最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知线段AD=10cm,线段AC=BD=6cm,F是线段CD的中点,求线段BF的长.
如图,已知线段AD=10cm,线段AC=BD=6cm,F是线段CD的中点,求线段BF的长. 如图,PA,PB是⊙O的两条切线,A,B是切点,连接AO并延长交⊙O于点C,交PB的延长线于点D.求证:OP∥BC.
如图,PA,PB是⊙O的两条切线,A,B是切点,连接AO并延长交⊙O于点C,交PB的延长线于点D.求证:OP∥BC. 如图,已知EO⊥AB于点O,OE平分∠MON,那么∠1与∠2相等吗?为什么?
如图,已知EO⊥AB于点O,OE平分∠MON,那么∠1与∠2相等吗?为什么?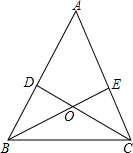 如图,△ABC中,BE,CD为角平分线且交点为点O,当∠A=60°时,
如图,△ABC中,BE,CD为角平分线且交点为点O,当∠A=60°时,