Question

8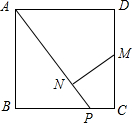．如图，P是正方形ABCD的边BC上一点，BP=3PC．M是CD的中点，MN⊥AP于N，求证：MN²=AN•PN．

Answer 1

分析 连接AM、PM，由正方形的性质得出AD=CD=BC，∠D=∠C=90°，由已知得出AD=CD=BC=4PC，AD=CD=2DM=2CM，得出$\frac{AD}{CM}=\frac{DM}{PC}$=2，证出△ADM∽△MCP，得出∠DAM=∠CMP，证出∠AMP=90°，由射影定理即可得出结论．

解答 证明：连接AM、PM，如图所示：∵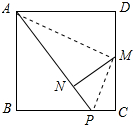
四边形ABCD是正方形，
∴AD=CD=BC，∠D=∠C=90°，
∵BP=3PC，
∴AD=CD=BC=4PC，
∵M是CD的中点，
∴AD=CD=2DM=2CM，
∴$\frac{AD}{CM}=\frac{DM}{PC}$=2，
∴△ADM∽△MCP，
∴∠DAM=∠CMP，
∴∠CMP+∠AMD=∠DAM+∠AMD=90°，
∴∠AMP=90°，
∵MN⊥AP，
∴由射影定理得：MN²=AN•PN．

点评 本题考查了正方形的性质、相似三角形的判定与性质；熟练掌握正方形的性质，证明三角形相似是解决问题的关键．