题目内容
13.已知关于x的一元二次方程x2-(2k+1)x+4k-3=0,求证:无论k为何值,此方程总有两个不等实根.分析 根据△=[-(2k+1)]2-4×1×(4k-3)=4(k-$\frac{3}{2}$)2+4>0判断即可.
解答 解:∵△=[-(2k+1)]2-4×1×(4k-3)
=4k2-12k+13
=4(k-$\frac{3}{2}$)2+4>0,
∴无论k为何值,此方程总有两个不等实根.
点评 本题主要考查根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1.计算$\frac{1}{14}$×(-14)÷(-$\frac{1}{14}$)×(-14)的结果是( )
| A. | 1 | B. | -196 | C. | 49 | D. | -49 |
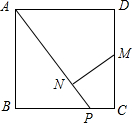 如图,P是正方形ABCD的边BC上一点,BP=3PC.M是CD的中点,MN⊥AP于N,求证:MN2=AN•PN.
如图,P是正方形ABCD的边BC上一点,BP=3PC.M是CD的中点,MN⊥AP于N,求证:MN2=AN•PN. 如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.
如图,P是∠AOB内一点,分别在OA、OB边上作点C、D,使得△PCD的周长最小.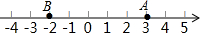 根据给出的数轴,回答下列问题
根据给出的数轴,回答下列问题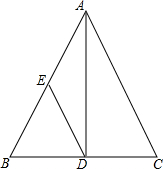 已知:如图,在△ABC中.AB=AC.点E是AB上一点.DE=AE,且DE∥AC.求证:AD是BC边上的中线.
已知:如图,在△ABC中.AB=AC.点E是AB上一点.DE=AE,且DE∥AC.求证:AD是BC边上的中线.