题目内容
17.在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.

分析 (1)根据题目要求补全图形即可;
(2)连接AE.由轴对称图形的性质可知EA=AB,∠ABF=∠AEF,由菱形的定义可知AB=AD,从而得到AE=AD,由等腰三角形的性质可知∠AEF=∠ADF,于是得到∠ABF=∠ADF;
(3)由轴对称图形的性质可知EF=BF,然后由DF=ED-EF,可知DF=ED-BF;
(4)由轴对称图形的性质可知EF=BF,然后由EF=ED+DF,可知BF=DE+DF.
解答 解:(1)如图1所示: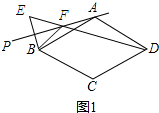
(2)∠ABF=∠ADF.
理由:如图2所示:连接AE.
∵点B与点E关于直线PA对称,
∴EA=AB,∠ABF=∠AEF.
∵四边形ABCD为菱形,
∴AB=AD.
∴AE=AD.
∴∠AEF=∠ADF.
∴∠ABF=∠ADF.
(3)DF=ED-BF.
理由:如图3所示: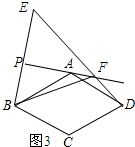
∵点B与点E关于PA对称,
∴EF=BF.
又∵DF=ED-EF,
∴DF=ED-BF.
(4)BF=DE+DF.
理由:如图4所示: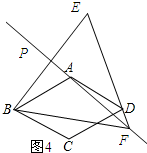
∵点B与点E关于PA对称,
∴EF=BF.
又∵EF=ED+DF,
∴BF=DE+DF.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了菱形的性质、轴对称图形的性质、等腰三角形的性质,由菱形的性质和轴对称图形的性质得到AE=AD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )
如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )
 如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )
如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )| A. | 16cm | B. | 18cm | C. | 30cm | D. | 2cm |
7.如图,这是一个立体图形从三个不同方向看到的平面图形,则这个立体图形可能是( )


| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 棱柱 |
 如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x.
如图,将边长为4的正方形ABCD折叠,使B点落在边AD上,记作B′(不与A、D重合)、EF为折痕,设AB′=x. 如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从$-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2}$中随机选取一个数记为a,则a的值既使得抛物线$y=\frac{1}{2}{x^2}+a$与扇形AOB的边界有公共点,又使得关于x的方程$\frac{ax+1}{x-2}=-1$的解是正数的概率是$\frac{1}{6}$.
如图,以扇形AOB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),∠AOB=45°.现从$-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2}$中随机选取一个数记为a,则a的值既使得抛物线$y=\frac{1}{2}{x^2}+a$与扇形AOB的边界有公共点,又使得关于x的方程$\frac{ax+1}{x-2}=-1$的解是正数的概率是$\frac{1}{6}$.