题目内容
11. 如图,梯子AB靠在墙上,梯子的底端 A到墙根 O 的距离为5m,梯子的顶端 B到地面的距离为12m,现将梯子的底端 A向外移动到 A′,使梯子的底端 A′到墙根O的距离等于6m,同时梯子的顶端 B下降至 B′,那么BB′( )
如图,梯子AB靠在墙上,梯子的底端 A到墙根 O 的距离为5m,梯子的顶端 B到地面的距离为12m,现将梯子的底端 A向外移动到 A′,使梯子的底端 A′到墙根O的距离等于6m,同时梯子的顶端 B下降至 B′,那么BB′( )| A. | 小于1 m | B. | 大于1 m | C. | 等于1 m | D. | 小于或等于1 m |
分析 在Rt△AOB中依据勾股定理可知AB2=169,在Rt△A′OB′中依据勾股定理可求得OB′的长,从而可求得BB′的长.
解答 解:在Rt△AOB中,由勾股定理可知AB2=AO2+OB2=169,
在Rt△A′OB′中由勾股定理可知A′B′2=A′O2+OB′2.
∵AB=A′B′,
∴A′O2+OB′2=13,
∴OB′=$\sqrt{169-36}$=$\sqrt{133}$,
∴BB′=OB-OB′=12-$\sqrt{133}$<1.
故选A.
点评 本题主要考查的是勾股定理的应用,关键是掌握勾股定理:直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
1.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a3)2=a6 | D. | (2a)2=2a2 |
3.探索规律:按照如图方式摆放餐桌和椅子.完成问题:

(1)填写如表:
(2)照这样的方式摆下去,写出摆第n个图形座位的总数;
解:第n个图形共有座位:4n+2个.

(1)填写如表:
| 图形编号 | (1) | (2) | (3) | (4) | … | (10) | … | (100) |
| 图中座位总数 | 6 | 10 | 14 | 18 | … | 42 | … | 402 |
解:第n个图形共有座位:4n+2个.




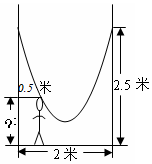 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为多少米?
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为多少米?