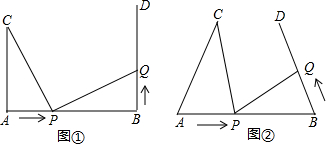��Ŀ����
6����֪��b����С���������������㣨c-5��2+|a+b|=0����1�������a��b��c��ֵ��
��2��a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����PΪ���㣬���Ӧ����Ϊx����P��0��2֮���˶�ʱ����0��x��2ʱ�����뻯��ʽ�ӣ�|x-3|+2|x+2|����д��������̣�
��3���ڣ�1������2�������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC-AB��ֵ�Ƿ�����ʱ��t�ı仯���仯�����仯����˵�����ɣ������䣬������ֵ��
���� ��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ����ĺ���0����ÿ������0���������a��b��c��ֵ��
��2������x�ķ�Χ��ȷ��x-3��x+2�ķ��ţ�Ȼ����ݾ���ֵ�����弴�ɻ���
��3������A��B��C���˶��������ȷ��AB��BC�ı仯���������ȷ��BC-AB��ֵ��
��� �⣺��1����������ã�c-5=0��a+b=0��b=1��
��a=-1��b=1��c=5��
��2����-2��x��3ʱ��x-3��0��x+2��0��
��|x-3|+2|x+2|=3-x+2x+4=7+x��
��x��3ʱ��x-3��0��x+2��0��
��|x-3|+2|x+2|=x-3+2x+4=3x+1��
��3��BC=5+5t-��1+2t��=3t+4��
AB=1+2t-��-1-t��=3t+2��
BC-AB=3t+4-��3t+2��=2��
��BC-AB��ֵ������ʱ��t�ı仯���ı䣬��ֵΪ2��
���� ���⿼�������������ֵ����ȷ����AB��BC�ı仯����ǹؼ���

��ϰ��ϵ�д�
 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
�����Ŀ
14������˵����ȷ���ǣ�������
| A�� | $\frac{2}{3}$��xy��ϵ����$\frac{2}{3}$ | B�� | 22xy2�Ĵ�����5 | ||
| C�� | $\frac{-x+1}{3}$�ij�������1 | D�� | 0�ǵ���ʽ |
1��������ʽ3amb4��-8bna2��ͬ�����m+n=��������
| A�� | -5 | B�� | 7 | C�� | 6 | D�� | 5 |
11�� ��ͼ������AB����ǽ�ϣ����ӵĵ� A��ǽ�� O �ľ���Ϊ5m�����ӵĶ��� B������ľ���Ϊ12m���ֽ����ӵĵ� A�����ƶ��� A�䣬ʹ���ӵĵ� A�䵽ǽ��O�ľ������6m��ͬʱ���ӵĶ��� B�½��� B�䣬��ôBB�䣨������
��ͼ������AB����ǽ�ϣ����ӵĵ� A��ǽ�� O �ľ���Ϊ5m�����ӵĶ��� B������ľ���Ϊ12m���ֽ����ӵĵ� A�����ƶ��� A�䣬ʹ���ӵĵ� A�䵽ǽ��O�ľ������6m��ͬʱ���ӵĶ��� B�½��� B�䣬��ôBB�䣨������
 ��ͼ������AB����ǽ�ϣ����ӵĵ� A��ǽ�� O �ľ���Ϊ5m�����ӵĶ��� B������ľ���Ϊ12m���ֽ����ӵĵ� A�����ƶ��� A�䣬ʹ���ӵĵ� A�䵽ǽ��O�ľ������6m��ͬʱ���ӵĶ��� B�½��� B�䣬��ôBB�䣨������
��ͼ������AB����ǽ�ϣ����ӵĵ� A��ǽ�� O �ľ���Ϊ5m�����ӵĶ��� B������ľ���Ϊ12m���ֽ����ӵĵ� A�����ƶ��� A�䣬ʹ���ӵĵ� A�䵽ǽ��O�ľ������6m��ͬʱ���ӵĶ��� B�½��� B�䣬��ôBB�䣨������| A�� | С��1 m | B�� | ����1 m | C�� | ����1 m | D�� | С�ڻ����1 m |
18�����и���ʽ����ͬ������ǣ�������
| A�� | 4x2y��4y2x | B�� | 2abc��2ab | C�� | $-\frac{3}{a}$ ��-3a | D�� | -x3y2��$\frac{1}{2}$y2x3 |