Question

1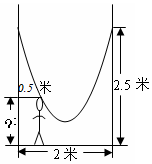．如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千．拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为多少米？

Answer 1

分析 根据题意建立直角坐标系，点（0，2.5）、（2，2.5）、（0.5，1）都在抛物线上，设抛物线解析式，列方程组，求解析式，根据解析式很容易就可求出抛物线的顶点坐标，纵坐标的绝对值即为绳子的最低点距地面的距离．

解答 解：以A为原点，AC所在直线为x轴，AB所在直线为y轴，建立如图所示的直角坐标系．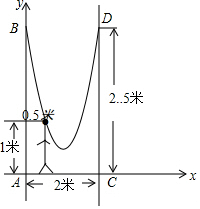

设抛物线的函数关系式为：y=ax²+bx+c．
将（0，2.5）、（2，2.5）、（0.5，1）代入y=ax²+bx+c得：
$\left\{\begin{array}{l}{c=2.5}\\{4a+2b+c=2.5}\\{\frac{1}{4}a+\frac{1}{2}b+c=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=2}\\{b=-4}\\{c=2.5}\end{array}\right.$．
∴抛物线的表达式为：y=2x²-4x+2.5；
∵y=2x²-4x+2.5=2（x-1）²+0.5
∴抛物线的顶点坐标为（1，0.5），
∴绳子的最低点距地面的距离为0.5m．

点评 本题主要考查函数解析式和点的坐标的求法，借助二次函数解决实际为题，本题关键在于正确选择原点建立直角坐标系，正确确定有关点的坐标，求出抛物线解析式．