题目内容
 某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.
某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.(1)求y与x关系式.
(2)该店老板计划这次选购A、B两种文具共100件,所花资金不超过1000元,并希望全部售完后获得不低于296元,若按A种文具日销售4件和B种文具每件可获利2元计算,老板这次有哪几种进货方案.
(3)若A中文具每件零售价比B种文具每件零售价高2元,求这两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间关系式.
考点:二次函数的应用
专题:
分析:(1)先设出一次函数,根据图形中的关系利用待定系数法求出关系式.
(2)根据题意设进货A种文具a件,则B种文具100-a件,由题中已知条件列出不等式,a取整数,找出否合题意的a即可;
(3)将两种文具的利润之和相加即可求得两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间关系式.
(2)根据题意设进货A种文具a件,则B种文具100-a件,由题中已知条件列出不等式,a取整数,找出否合题意的a即可;
(3)将两种文具的利润之和相加即可求得两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间关系式.
解答:解:(1)设y=kx+b,
由题意得,直线过(10,10)和(15,5),
代入方程得
,
∴得出k=-1,b=20,
∴y=-x+20.
(2)设进货A种文具a件,则B种文具100-a件,
则由题意知:
,
解得48≤a≤50,
由a为整数,则有a=48,b=52;a=49,b=51;a=50,b=50三种情况,
即他这次有三种进货方式;
(3)销售利润W=(x-12)(-x+20)+(x-10)(-x+22)=-2x2+64x-460.
由题意得,直线过(10,10)和(15,5),
代入方程得
|
∴得出k=-1,b=20,
∴y=-x+20.
(2)设进货A种文具a件,则B种文具100-a件,
则由题意知:
|
解得48≤a≤50,
由a为整数,则有a=48,b=52;a=49,b=51;a=50,b=50三种情况,
即他这次有三种进货方式;
(3)销售利润W=(x-12)(-x+20)+(x-10)(-x+22)=-2x2+64x-460.
点评:此题考查了二次函数的应用,一元一次不等式组的应用,以及待定系数法确定函数解析式,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
相关题目
-4的倒数是( )
A、-
| ||
B、
| ||
| C、-4 | ||
| D、4 |
 一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,木杆折断以前有多少米?
一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,木杆折断以前有多少米? 大小正方形如图,小正方形边长为acm,大正方形边长为bcm,阴影面积是
大小正方形如图,小正方形边长为acm,大正方形边长为bcm,阴影面积是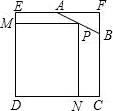 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积. 如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于