题目内容
 把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=
把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=| 1 |
| 3 |
考点:两点间的距离
专题:
分析:分类讨论:AP是最短的一段时,BP是最短的一段时,根据最短一段的绳长,可得AP的长,根据线段中点的性质,可得原绳长.
解答:解:①当AP是最短的一段时,AP=20cm,由AP=
PB,得
PB=3AP,
由线段的和差,得
AB=AP+PB=4AP,
由B为原绳长的中点,得
原绳长是8AP=8×20=160cm,
②BP是最短的一段时,PB=3AP=20,
解得AP=
由线段的和差,得
AB=AP+PB=4AP,
由A为原绳长的中点,得
原绳长是8AP=8AP=
×8=
cm.
综上所述:原绳长
cm或160cm.
| 1 |
| 3 |
PB=3AP,
由线段的和差,得
AB=AP+PB=4AP,
由B为原绳长的中点,得
原绳长是8AP=8×20=160cm,
②BP是最短的一段时,PB=3AP=20,
解得AP=
| 20 |
| 3 |
由线段的和差,得
AB=AP+PB=4AP,
由A为原绳长的中点,得
原绳长是8AP=8AP=
| 20 |
| 3 |
| 160 |
| 3 |
综上所述:原绳长
| 160 |
| 3 |
点评:本题考查了两点间的距离,分类讨论是解题关键,以防遗漏.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
有一位工人师傅将底面直径是10cm,高为80cm的“瘦长”形圆柱,锻造成底面直径为40cm的“矮胖”形圆柱,则“矮胖”形圆柱的高是( )
| A、4cm | B、5cm |
| C、6cm | D、7cm |
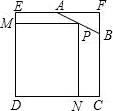 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积. 如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是
如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于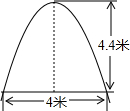 某工厂大门是抛物线形水泥建筑,大门地面宽为4m,顶部距离地面的高度为4.4m,
某工厂大门是抛物线形水泥建筑,大门地面宽为4m,顶部距离地面的高度为4.4m, 已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N当扇形CEF绕点C在∠ACB的内部旋转时,如图,求证:MN2=AM2+BN2.
已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N当扇形CEF绕点C在∠ACB的内部旋转时,如图,求证:MN2=AM2+BN2.