题目内容
如图所示,已知点O为△ABC的内心,连AO、BO、CO,过点O的直线分别交边AB、AC于点M、N,
(1)若∠BAC=70°,那么∠BOC= °;
(2)如图1所示,若MN∥BC,BM=2,CN=3,求线段MN的长;
(3)如图2所示,若MN⊥AO,BM=2,CN=3,求线段MN的长.

(1)若∠BAC=70°,那么∠BOC=
(2)如图1所示,若MN∥BC,BM=2,CN=3,求线段MN的长;
(3)如图2所示,若MN⊥AO,BM=2,CN=3,求线段MN的长.

考点:相似三角形的判定与性质,角平分线的定义,平行线的性质,等腰三角形的判定与性质
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB=110°,根据三角形的内心求出∠OBC=
∠ABC,∠OCB=
∠ACB,求出∠OBC+∠OCB=55°,即可得出答案;
(2)根据平行线的性质求出∠MOB=∠OBC,求出∠MOB=∠ABO,根据等腰三角形的判定得出BM=MO,同理NO=CN=3,求出即可;
(3)求出∠5=∠7,根据三角形的内心求出∠4=∠6=
∠BAC,∠12=∠10=
∠ABC,∠8=∠9=
∠ACB,求出∠1=∠2=∠3,∠10=∠11=∠12,根据相似三角形的判定得出△MBO∽△NOC,根据相似三角形的性质得出
=
,代入求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据平行线的性质求出∠MOB=∠OBC,求出∠MOB=∠ABO,根据等腰三角形的判定得出BM=MO,同理NO=CN=3,求出即可;
(3)求出∠5=∠7,根据三角形的内心求出∠4=∠6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MB |
| NO |
| MO |
| NC |
解答: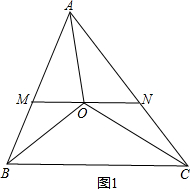 解:(1)如图1,∵∠BAC=70°,
解:(1)如图1,∵∠BAC=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴点O为△ABC的内心,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
×110°=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°,
故答案为:125°;
(2)∵MN∥BC,
∴∠MOB=∠OBC,
∵O为△ABC的内心,
∴∠ABO=∠OBC,
∴∠MOB=∠ABO,
∴BM=MO,
∵BM=2,
∴MO=2,
同理NO=CN=3,
∴MN=2+3=5,
即MN=5;
(3)如图2,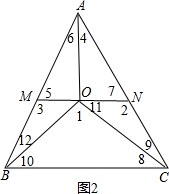
∵AO⊥MN,O为△ABC的内心,
∴∠4=∠6,∠AOM=∠AON=90°,
∴∠5=∠7,
∵∠3+∠5=180°,∠2+∠7=180°,
∴∠2=∠3,
∵O为△ABC的内心,
∴∠4=∠6=
∠BAC,∠12=∠10=
∠ABC,∠8=∠9=
∠ACB,
∴∠1=180°-(∠10+∠8)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠BAC)
=90°+
∠BAC
=90°+∠4,
∠2=180°-∠7
=180°-
(180°-∠BAC)
=90°+
∠BAC
=90°+∠4,
∴∠1=∠2=∠3,
∵∠1+∠8+∠10=180°,∠2+∠11+∠9=180°,
∵∠8=∠9,
∴∠10=∠11=∠12,
∴△MBO∽△NOC,
∴
=
,
∵OM=ON,MB=2,NC=3,
∴MO2=MB•CN=6,
∴MO=
,
∴MN=2
.
 解:(1)如图1,∵∠BAC=70°,
解:(1)如图1,∵∠BAC=70°,∴∠ABC+∠ACB=180°-70°=110°,
∴点O为△ABC的内心,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°,
故答案为:125°;
(2)∵MN∥BC,
∴∠MOB=∠OBC,
∵O为△ABC的内心,
∴∠ABO=∠OBC,
∴∠MOB=∠ABO,
∴BM=MO,
∵BM=2,
∴MO=2,
同理NO=CN=3,
∴MN=2+3=5,
即MN=5;
(3)如图2,

∵AO⊥MN,O为△ABC的内心,
∴∠4=∠6,∠AOM=∠AON=90°,
∴∠5=∠7,
∵∠3+∠5=180°,∠2+∠7=180°,
∴∠2=∠3,
∵O为△ABC的内心,
∴∠4=∠6=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=180°-(∠10+∠8)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=90°+∠4,
∠2=180°-∠7
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=90°+∠4,
∴∠1=∠2=∠3,
∵∠1+∠8+∠10=180°,∠2+∠11+∠9=180°,
∵∠8=∠9,
∴∠10=∠11=∠12,
∴△MBO∽△NOC,
∴
| MB |
| NO |
| MO |
| NC |
∵OM=ON,MB=2,NC=3,
∴MO2=MB•CN=6,
∴MO=
| 6 |
∴MN=2
| 6 |
点评:本题考查了等腰三角形的性质和判定,平行线的性质,相似三角形的性质和判定,三角形的内心和内切圆,三角形的内角和定理的应用,能综合运用所学性质进行推理是解此题的关键,综合性比较强,难度偏大.

练习册系列答案
相关题目
求1+2+22+23+…+22014的值,可令S=1+2+22+23+…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,仿照以上推理,计算出1+5+52+53+…+52013的值为( )
| A、52014-1 | ||
| B、52015-1 | ||
C、
| ||
D、
|
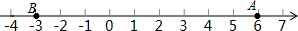 如图,已知数轴上点A表示的数为6,点B表示的数为-3,C为线段AB上一点,且AC=2BC,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,点B表示的数为-3,C为线段AB上一点,且AC=2BC,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.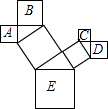 如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.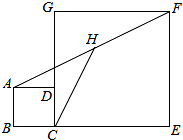 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 把两个三角尺ABC与DEF按如图所示那样拼在一起,其中点D在BC上,DM为∠CDE的平分线,DN为∠BDF的平分线,则∠MDN的度数是
把两个三角尺ABC与DEF按如图所示那样拼在一起,其中点D在BC上,DM为∠CDE的平分线,DN为∠BDF的平分线,则∠MDN的度数是