题目内容
 把两个三角尺ABC与DEF按如图所示那样拼在一起,其中点D在BC上,DM为∠CDE的平分线,DN为∠BDF的平分线,则∠MDN的度数是
把两个三角尺ABC与DEF按如图所示那样拼在一起,其中点D在BC上,DM为∠CDE的平分线,DN为∠BDF的平分线,则∠MDN的度数是考点:角平分线的定义
专题:
分析:根据∠EDF=90°,可得出∠CDE+∠BDF=90°,再根据DM为∠CDE的平分线,DN为∠BDF的平分线,可得出∠CDM+∠BDF=45°,从而得出∠MDN的度数.
解答:解:∵∠EDF=90°,
∴∠CDE+∠BDF=90°,
∵DM为∠CDE的平分线,DN为∠BDF的平分线,
∴∠MDE=
∠CDE,∠FDN=
∠BDF,
∴∠CDM+∠BDF=
(∠CDE+∠BDF)=
×90°=45°,
∴∠MDN=180°-45°=135°,
故答案为135°.
∴∠CDE+∠BDF=90°,
∵DM为∠CDE的平分线,DN为∠BDF的平分线,
∴∠MDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CDM+∠BDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MDN=180°-45°=135°,
故答案为135°.
点评:本题考查了角平分线的定义,求得∠CDE+∠BDF=90°是解题的关键.

练习册系列答案
相关题目
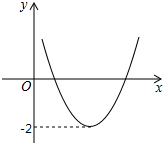 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )| A、k<2 | B、k>2 |
| C、0<k<2 | D、-2<k<2 |
下列说法正确的是( )
| A、1是最小的整数 |
| B、-1是最大的负整数 |
| C、绝对值是它本身的只有正数 |
| D、负数的相反数可能是负数 |

 找出图中所有的同位角、内错角、同旁内角.
找出图中所有的同位角、内错角、同旁内角. 如图,已知tanO=
如图,已知tanO= 某人在河旁高4米的土堆CD的顶端D观察河对岸树AB的顶部A仰角为30°,树顶A的倒影F俯角为45°,求树高.
某人在河旁高4米的土堆CD的顶端D观察河对岸树AB的顶部A仰角为30°,树顶A的倒影F俯角为45°,求树高. 如图,AB=AD,∠1=∠2,∠B=∠ADE,且点D在BC边上,DE与AC相交于点F.求证:△ABC≌△ADE.
如图,AB=AD,∠1=∠2,∠B=∠ADE,且点D在BC边上,DE与AC相交于点F.求证:△ABC≌△ADE.