题目内容
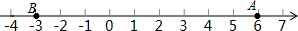 如图,已知数轴上点A表示的数为6,点B表示的数为-3,C为线段AB上一点,且AC=2BC,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,点B表示的数为-3,C为线段AB上一点,且AC=2BC,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)数轴上点C表示的数是
(2)当t=2时,线段PC的长为
(3)当点P为AC的中点时,t=
(4)当t=
考点:一元一次方程的应用,数轴,两点间的距离
专题:
分析:(1)根据两点间的距离可以求得点C、P所表示的数;
(2)(3)由“路程=速度×时间”进行计算;
(4)需要分类讨论:点P在点A的左边和右边两种情况.
(2)(3)由“路程=速度×时间”进行计算;
(4)需要分类讨论:点P在点A的左边和右边两种情况.
解答:解:(1)设点C表示的数为x,则
6-x=2[x-(-3)],
解得 x=0,
即点C表示的数是0.
点P表示是数是:2t-3.
故答案是:0;2t-3;
(2)当t=2时,点P表示是数是:2×2-3=1,
则PC=1-0=1.
故答案是:1;
(3)∵点A、C分别表示6、0,点P为AC的中点,
∴点P表示的数是3.
∴3=2t-3,
解得 t=3.
故答案是:3;
(4)当点P在点A的左边时,2t-3=2[6-(2t-3)],
解得 t=3.5;
当点P在点A的右边时,2t-3=2[(2t-3)-6],
解得 t=7.5;
综上所述,t的值是3.5或7.5.
故答案是:3.5或7.5.
6-x=2[x-(-3)],
解得 x=0,
即点C表示的数是0.
点P表示是数是:2t-3.
故答案是:0;2t-3;
(2)当t=2时,点P表示是数是:2×2-3=1,
则PC=1-0=1.

故答案是:1;
(3)∵点A、C分别表示6、0,点P为AC的中点,
∴点P表示的数是3.
∴3=2t-3,
解得 t=3.
故答案是:3;
(4)当点P在点A的左边时,2t-3=2[6-(2t-3)],
解得 t=3.5;
当点P在点A的右边时,2t-3=2[(2t-3)-6],
解得 t=7.5;
综上所述,t的值是3.5或7.5.
故答案是:3.5或7.5.
点评:本题考查了一元一次方程的应用、数轴以及两点间的距离.解答第(4)题时,要对点P的位置进行分类讨论,以防漏解.

练习册系列答案
相关题目
相反数为3的数是( )
| A、-3 | ||
| B、3 | ||
| C、9 | ||
D、
|
在π,
,
,0,
,0.010010001…(相邻两个1之间0的个数在递增)中,无理数有( )
| 22 |
| 7 |
| 3 | 8 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
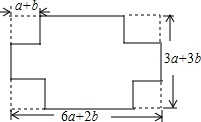 如图,李师傅把一块长方形(边长分别为6a+2b和3a+3b)铁皮的四个角各剪去一个边长为(a+b)的小正方形,然后折成一个无盖的盒子.
如图,李师傅把一块长方形(边长分别为6a+2b和3a+3b)铁皮的四个角各剪去一个边长为(a+b)的小正方形,然后折成一个无盖的盒子.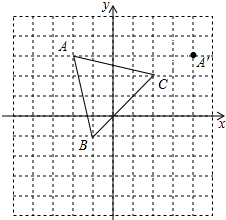 在平面直角坐标系中,△ABC的三个顶点的位置如图所示(顶点在格点上).现将△ABC沿某直线翻折,使点A变换为点A′,A点坐标为(-2,3),A′的坐标为(4,3).
在平面直角坐标系中,△ABC的三个顶点的位置如图所示(顶点在格点上).现将△ABC沿某直线翻折,使点A变换为点A′,A点坐标为(-2,3),A′的坐标为(4,3). P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为
P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为