题目内容
5. 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )| A. | abc>0 | B. | a+b+c>0 | C. | c<0 | D. | b<0 |
分析 利用抛物线开口方向得到a<0,利用抛物线的对称轴位置得到b<0,利用抛物线与x轴的交点位置得到c>0,则可对A、B、C进行判断;利用x=1时,y>0,可对B进行判断.
解答 解:抛物线开口向下,则a<0,抛物线的对称轴在y轴的右侧,则b<0,抛物线与x轴的交点在x轴上方,则c>0,
所以A选项,C选项、D选项都错误;
由于x=1时,y>0,即a+b+c>0,所以C选项正确.
故选B.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置;当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).抛物线与x轴交点个数.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
15.在如图的2016年11月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )


| A. | 27 | B. | 51 | C. | 69 | D. | 72 |
16.下列各组中的两项是同类项的是( )
| A. | 16zy2和-12y2z | B. | -m2n和mn2 | C. | -x2和3x | D. | 0.5a和0.5b |
 某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )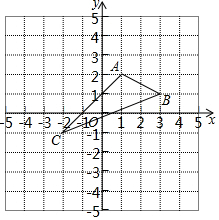 如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).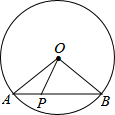 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.