题目内容
2.已知抛物线的对称轴是直线x=2,顶点在直线y=x-1上,并且经过点(3,-8)(1)求这条抛物线的函数表达式.
(2)写出这条抛物线与坐标轴的交点坐标.
分析 (1)根据题意求得该抛物线的顶点坐标,然后设抛物线的函数式是顶点式,将点(3,-8)代入求系数的值即可;
(2)根据(1)中求得的抛物线解析式来求抛物线与坐标轴的交点坐标.
解答 解:(1)∵抛物线的对称轴是直线x=2,顶点在直线y=x-1上,
∴该抛物线的顶点坐标是(2,1).
故设该抛物线的解析式为y=a(x-2)2+1.
把x=3,y=-8代入,得
-8=a(3-2)2+1.
解得a=-9.
故该抛物线的解析式是y=-9(x-2)2+1或y=-9x2+36x-35.
(2)由(1)知,该抛物线的解析式是y=-9(x-2)2+1.
令x=0,则y=-35.
令y=0,则x=$\frac{7}{3}$或x=$\frac{5}{3}$.
所以抛物线与坐标轴的交点坐标是(0,-35)、($\frac{7}{3}$,0)、($\frac{5}{3}$,0).
点评 本题考查了抛物线与x轴的交点坐标,一次函数图象上点的坐标特征以及待定系数法求二次函数的解析式.熟练掌握二次函数的三种形式,可以选择适当的方法求二次函数解析式.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
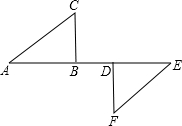 如图,点A,B,D,E在同一条直线上,AD=EB,BC∥DF,∠C=∠F,试判断△ABC与△EDF是否全等,并说明理由.
如图,点A,B,D,E在同一条直线上,AD=EB,BC∥DF,∠C=∠F,试判断△ABC与△EDF是否全等,并说明理由.