题目内容
已知圆锥底面半径为r，若它的侧面积是底面积的1.5倍，则母线长 ，展开后扇形的圆心角为 ．
考点：圆锥的计算
专题：
分析：设圆锥的母线长为l，用圆锥的底面积表示出其侧面积，从而用r表示出圆锥的母线长，然后利用扇形的弧长等于圆锥的底面周长求得其圆心角即可．
解答：解：设圆锥的母线长为l，
∵圆锥底面半径为r，若它的侧面积是底面积的1.5倍，
∴圆锥的侧面积为1.5πr2，
∴πrl=1.5πr2，
解得：l=1.5r，
根据弧长公式得：2πr=
，
解得：n=240，
故答案为：1.5r，240°．
∵圆锥底面半径为r，若它的侧面积是底面积的1.5倍，
∴圆锥的侧面积为1.5πr2，
∴πrl=1.5πr2，
解得：l=1.5r，
根据弧长公式得：2πr=
| nπ×1.5r |
| 180 |
解得：n=240，
故答案为：1.5r，240°．
点评：本题考查了圆锥的计算，解题的关键是牢记有关圆锥的公式，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中不正确的是（ ）
| A、在同一平面内，经过一点能画一条且只能画一条直线与已知直线垂直 |
| B、从直线外一点到这条直线的垂线段叫做点到直线的距离 |
| C、一条直线的垂线可以画无数条 |
| D、连接直线外一点与直线上各点的所有线段中，垂线段最短 |
如图，AB为⊙O的固定直径，过⊙O上一点作CD⊥AB，交⊙O于D，∠OCD的平分线交⊙O于P，到C点在半圆上（不包括A、B两点）移动时，点P的位置是否发生改变？请说明理由．
如图，在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着，其中AB这根木棒的影子是BE．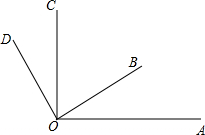
如图，已知∠AOC与∠BOD都是直角，∠BOC=59°