题目内容
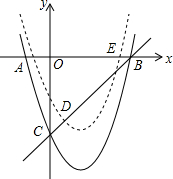 如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.
如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.考点:二次函数图象与几何变换
专题:
分析:首先求出抛物线与坐标轴交点坐标,求出直线BC的解析式,进而利用函数有两个交点,利用根的判别式得出k的取值范围.
解答: 解:∵抛物线y=x2-2x-3与x轴交于A,B两点,与x轴交于点C点,
解:∵抛物线y=x2-2x-3与x轴交于A,B两点,与x轴交于点C点,
∴y=0时,0=x2-2x-3
解得:x1=-1,x2=3,
故A(-1,0),B(3,0),
当x=0,y=-3,
故C(0,-3),
设直线BC的解析式为:y=kx+b,
则
,
解得:
,
故直线BC的解析式为:y=x-3,
设平移后解析式为:y=x2-2x-3+k,
则
,
则x-3=x2-2x-3+k,
x2-3x+k=0,
∵将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,
∴△=b2-4ac=9-4k>0,
则k<
,
故k的取值范围是:0<k<
.
 解:∵抛物线y=x2-2x-3与x轴交于A,B两点,与x轴交于点C点,
解:∵抛物线y=x2-2x-3与x轴交于A,B两点,与x轴交于点C点,∴y=0时,0=x2-2x-3
解得:x1=-1,x2=3,
故A(-1,0),B(3,0),
当x=0,y=-3,
故C(0,-3),
设直线BC的解析式为:y=kx+b,
则
|
解得:
|
故直线BC的解析式为:y=x-3,
设平移后解析式为:y=x2-2x-3+k,
则
|
则x-3=x2-2x-3+k,
x2-3x+k=0,
∵将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,
∴△=b2-4ac=9-4k>0,
则k<
| 9 |
| 4 |
故k的取值范围是:0<k<
| 9 |
| 4 |
点评:此题主要考查了二次函数图象与几何变换以及待定系数法求一次函数解析式,得出△=b2-4ac=9-4k>0是解题关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
下列各式子中,其值一定是正数的是(其中a,b为有理数)( )
| A、a2+b2 |
| B、a3+1 |
| C、(a+b)2 |
| D、a2+1 |
已知一正方形的内切圆半径为1,那么这个正方形与它的内切圆及外接圆的面积的比为( )
| A、4:1:2 |
| B、4:2π:π |
| C、4:2π:1 |
| D、4:π:2π |
 如图,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I是( )
如图,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I是( )| A、60° | B、80° |
| C、90° | D、100° |
 如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.
如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.