题目内容
 如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.
如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.(1)求S与x的函数关系式及x的取值范围.
(2)如果要围成的花圃ABCD的面积是45平方米,则AB的长为多少米?
考点:一元二次方程的应用,根据实际问题列二次函数关系式
专题:
分析:(1)已知AB=x,BC=24-3x,则y=-3x2+24x.易求x的取值范围.
(2)当y=45时,根据实际情况求出x的值即可.
(2)当y=45时,根据实际情况求出x的值即可.
解答:解:(1)S=(24-3x)x=24x-3x2;
又∵x>0,且10≥24-3x>0,
∴
≤x<8;
(2)依题意有45=24x-3x2,
x=5或x=3;
若x=3,则AB=3m,则BC=15m>10m,舍去.
答:AB的长为5米.
又∵x>0,且10≥24-3x>0,
∴
| 14 |
| 3 |
(2)依题意有45=24x-3x2,
x=5或x=3;
若x=3,则AB=3m,则BC=15m>10m,舍去.
答:AB的长为5米.
点评:考查了一元二次方程的应用解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的关键是垂直于墙的有三道篱笆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中正确的是( )
| A、两个平行四边形一定相似 |
| B、两个菱形一定相似 |
| C、两个矩形一定相似 |
| D、两个等腰直角三角形一定相似 |
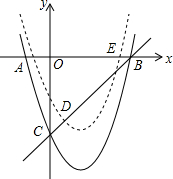 如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.
如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠OCB的度数等于
如图,⊙O是△ABC的外接圆,∠A=50°,则∠OCB的度数等于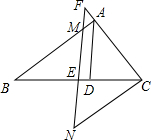 如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F,CN∥AB交FE的延长线于N,求证:BM=CF.
如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F,CN∥AB交FE的延长线于N,求证:BM=CF.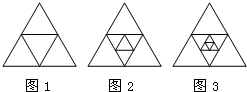 如图,在图1中,互不重叠的三角形共有4个,在图,2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第9个图形中,互不重叠的三角形共有
如图,在图1中,互不重叠的三角形共有4个,在图,2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第9个图形中,互不重叠的三角形共有