题目内容
已知一正方形的内切圆半径为1,那么这个正方形与它的内切圆及外接圆的面积的比为( )
| A、4:1:2 |
| B、4:2π:π |
| C、4:2π:1 |
| D、4:π:2π |
考点:正多边形和圆
专题:
分析:利用正方形的内切圆半径为1,可求出正方形的边长及正方形内切圆与外接圆的半径,再求出各自的面积,即可求出正方形与它的内切圆及外接圆的面积的比.
解答:解:如图:

∵正方形的内切圆半径为1,
∴AD=2,AO=
.
∴S正方形ABCD=2×2=4,S正方形内切圆=π,S正方形外接圆=2π,
∴S正方形ABCD:S正方形内切圆:S正方形外接圆=4:π:2π.
故选:D.

∵正方形的内切圆半径为1,
∴AD=2,AO=
| 2 |
∴S正方形ABCD=2×2=4,S正方形内切圆=π,S正方形外接圆=2π,
∴S正方形ABCD:S正方形内切圆:S正方形外接圆=4:π:2π.
故选:D.
点评:本题主要考查了正多边形和圆,解题的关键是求出正方形的边长及正方形内切圆与外接圆的半径.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0;②2a+b<0;③4a-2b+c=0;④9a+3b+c=0,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0;②2a+b<0;③4a-2b+c=0;④9a+3b+c=0,其中正确的是( )| A、①② | B、②③ | C、③④ | D、①④ |
下列说法中正确的是( )
| A、两个平行四边形一定相似 |
| B、两个菱形一定相似 |
| C、两个矩形一定相似 |
| D、两个等腰直角三角形一定相似 |
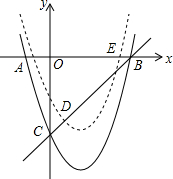 如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.
如图,已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C点,将抛物线沿对称轴向上平移k个单位长度后与线段BC交于D,E两个不同的点,求k的取值范围.