题目内容
 已知反比例函数y=
已知反比例函数y=| m+4 |
| x |
(1)求m的值;
(2)如图,过点A作直线AC与函数y=
| m+4 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点坐标代入反比例函数解析式可求得m;
(2)设直线AB的解析式为y=kx+b,可表示出C点坐标,再表示出B点坐标,代入反比例函数解析式可得到k、b的方程,且A点在直线上,可得到关于k、b的方程组,求解即可.
(2)设直线AB的解析式为y=kx+b,可表示出C点坐标,再表示出B点坐标,代入反比例函数解析式可得到k、b的方程,且A点在直线上,可得到关于k、b的方程组,求解即可.
解答:解:(1)∵反比例函数图象过点A(2,6),
∴m+4=12,
解得m=8;
(2)设直线AB的解析式为y=kx+b,
令y=0可得x=-
,即C点为(-
,0),
∵B为AC的中点,
∴B点坐标为(1-
,3),
又∵B在反比例函数图象上,且由(1)可知反比例函数解析式为y=
,
∴3(1-
)=12,整理可得b=-6k①,
又∵A点在直线AB上,代入y=kx+b可得2k+b=6②,
①代入②可得k=-
,b=9,
∴直线AB解析式为y=-
x+9.
∴m+4=12,
解得m=8;
(2)设直线AB的解析式为y=kx+b,
令y=0可得x=-
| b |
| k |
| b |
| k |
∵B为AC的中点,
∴B点坐标为(1-
| b |
| 2k |
又∵B在反比例函数图象上,且由(1)可知反比例函数解析式为y=
| 12 |
| x |
∴3(1-
| b |
| 2k |
又∵A点在直线AB上,代入y=kx+b可得2k+b=6②,
①代入②可得k=-
| 3 |
| 2 |
∴直线AB解析式为y=-
| 3 |
| 2 |
点评:本题主要考查待定系数法求函数解析式和函数的交点,掌握图象上点的坐标满足函数解析式和中点坐标公式是解题的关键.

练习册系列答案
相关题目
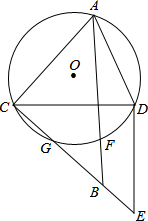 已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.
已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.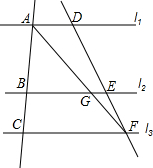 如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.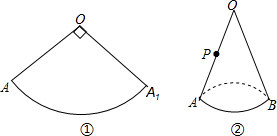
 如图,角的顶点是
如图,角的顶点是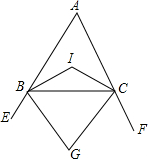 如图,在△ABC中,BI和CI分别平分∠ABC和∠ACB且交于点I,BG和CG分别平分∠CBE和∠BCF且交于点G,求证:∠BIC=
如图,在△ABC中,BI和CI分别平分∠ABC和∠ACB且交于点I,BG和CG分别平分∠CBE和∠BCF且交于点G,求证:∠BIC=