Question

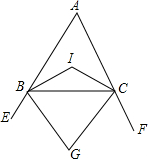如图，在△ABC中，BI和CI分别平分∠ABC和∠ACB且交于点I，BG和CG分别平分∠CBE和∠BCF且交于点G，求证：∠BIC=

1

2

∠A+90°．

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：证明题

分析：根据三角形的内角和等于180°表示出∠ABC+∠ACB，再根据角平分线的定义表示出∠IBC+∠ICB，然后利用三角形的内角和定理列式整理即可得证．

解答：证明：在△ABC中，∠ABC+∠ACB=180°-∠A，
∵BI和CI分别平分∠ABC和∠ACB且交于点I，
∴∠IBC+∠ICB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A），
在△BIC中，∠BIC=180°-（∠IBC+∠ICB）=180°-

1

2

（180°-∠A）=

1

2

∠A+90°，
即：∠BIC=

1

2

∠A+90°．

点评：本题考查了三角形的内角和定理，角平分线的定义，整体思想的利用是解题的关键．