题目内容
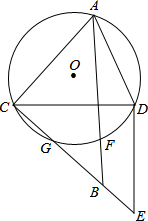 已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.
已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.考点:三角形的内切圆与内心
专题:证明题
分析:根据连接CF、DF、BD,可得出∠CDF=∠CAF=45°,则DF平分∠CDE,再根据CD=CB,得∠CDB=∠CBD,从而得出∠CDF=∠CAF=∠CBA,即可得出△CDF≌△CBF,则CF平分∠DCE,即可得出F为△CDE的内心.
解答: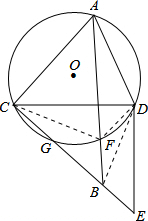 证明:连接CF、DF、BD,
证明:连接CF、DF、BD,
∵∠ACB=90°,CA=CB,
∴∠CAB=∠CBA=45°
∴∠CDF=∠CAF=45°,
∴∠EDF=∠CDE-∠CDF=45°,
∴DF平分∠CDE,
∵CB=CD,
∴∠CDB=∠CBD,
∵∠CDF=∠CAF=∠CBA,
∴∠FDB=∠FBD,
∴DF=BF,
∵CD=CB,CF=CF,
在△CDF和△CBF中,
,
∴△CDF≌△CBF(SAS),
∴∠DCF=∠BCF,
∴CF平分∠DCE,
∴点F是△CDF内心.
 证明:连接CF、DF、BD,
证明:连接CF、DF、BD,∵∠ACB=90°,CA=CB,
∴∠CAB=∠CBA=45°
∴∠CDF=∠CAF=45°,
∴∠EDF=∠CDE-∠CDF=45°,
∴DF平分∠CDE,
∵CB=CD,
∴∠CDB=∠CBD,
∵∠CDF=∠CAF=∠CBA,
∴∠FDB=∠FBD,
∴DF=BF,
∵CD=CB,CF=CF,
在△CDF和△CBF中,
|
∴△CDF≌△CBF(SAS),
∴∠DCF=∠BCF,
∴CF平分∠DCE,
∴点F是△CDF内心.
点评:本题考查了三角形的内切圆与内心,以及全等三角形的判定和性质,是中考常见题型,失分较多.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
比较∠CAB与∠DAB时,把它们的顶点A和边AB重合,把∠CAB和∠DAB放在AB的同一侧,若∠CAB>∠DAB,则( )
| A、AD落在∠CAB的内部 |
| B、AD落在∠CAB的外部 |
| C、AC和AD重合 |
| D、不能确定AD的位置 |
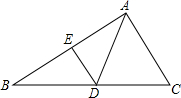 如图,△ABC中,AD=DB,∠EDB=∠DAC,求证:△ABC∽△EAD.
如图,△ABC中,AD=DB,∠EDB=∠DAC,求证:△ABC∽△EAD. 如图,某中学有一道长为35米的墙,计划用60米长的围栏靠墙围成一个面积为400平方米的矩形草坪ABCD,求该矩形草坪BC边的长.
如图,某中学有一道长为35米的墙,计划用60米长的围栏靠墙围成一个面积为400平方米的矩形草坪ABCD,求该矩形草坪BC边的长.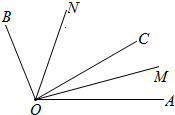 如图,射线OC在∠AOB的内部,射线OM是∠AOC的平分线,射线ON是∠BOC的平分线.
如图,射线OC在∠AOB的内部,射线OM是∠AOC的平分线,射线ON是∠BOC的平分线. 已知反比例函数y=
已知反比例函数y=