题目内容
11.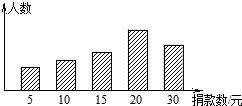 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.(1)孔明同学调查的这组学生共有60人;
(2)这组数据的众数是20元,中位数是20元;
(3)若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?
分析 (1)利用从左到右各长方形高度之比为3:4:5:10:8,可设捐5元、10元、15元、20元和30元的人数分别为3x、4x、5x、10x、8x,则根据题意得8x=16,解得x=2,然后计算3x+4x+5x++10x+8x即可;
(2)先确定各组的人数,然后根据中位数和众数的定义求解;
(3)先计算出样本的加权平均数,然后利用样本平均数估计总体,用2000乘以样本平均数即可.
解答 解:(1)设捐5元、10元、15元、20元和30元的人数分别为3x、4x、5x、10x、8x,
8x=16,
解得x=2,
∴3x+4x+5x+10x+8x=30x=20×2=60(人);
(2)捐5元、10元、15元、20元和30元的人数分别为6,8,10,20,16,
∵20出现次数最多,
∴众数为20元;
∵共有60个数据,第30个和第31个数据落在第四组内,
∴中位数为20元;
(3)$\frac{5×6+10×8+15×10+20×20+30×16}{60}$×2000=38000(元),
∴估算全校学生共捐款38000元.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.也考查了样本估计总体、中位数与众数.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
1. 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )| A. | BC=FD,AC=ED | B. | ∠A=∠DEF,AC=ED | C. | AC=ED,AB=EF | D. | ∠ABC=∠EFD,BC=FD |
16.将分式方程$\frac{x}{x-3}=2-\frac{3}{3-x}$去分母得( )
| A. | x=2+3 | B. | x=2(x-3)+3 | C. | x=2(x-3)+3(x-3) | D. | x=2(x-3)-3 |
 如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有( )个.
如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有( )个.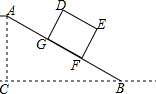 如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号) 如图所示,一次课外活动中,小李同学在离旗杆AB底部10米远的C处,用测角仪测得旗杆顶部A的仰角为60°,已知测角仪器的高CD=1米,求旗杆AB的高.
如图所示,一次课外活动中,小李同学在离旗杆AB底部10米远的C处,用测角仪测得旗杆顶部A的仰角为60°,已知测角仪器的高CD=1米,求旗杆AB的高. 如图所示,正比例函数与反比例函数的图象相交于A、B两点,过点A作AC∥y轴交x轴于点C,过点D作DM∥x轴交双曲线y=$\frac{k}{x}$于点E,交直线AC于点M(4,2),得到四边形OAME的面积为4.
如图所示,正比例函数与反比例函数的图象相交于A、B两点,过点A作AC∥y轴交x轴于点C,过点D作DM∥x轴交双曲线y=$\frac{k}{x}$于点E,交直线AC于点M(4,2),得到四边形OAME的面积为4. 如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.
如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.