题目内容
7．
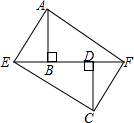如图所示，AB⊥EF于B，CD⊥EF于D，AF=CE，BE=DF，求证：AE=CF．
分析 首先证明△EDC≌△FBA，推出∠DEC=∠AFB，AF∥BC，接下来只要证明四边形AECF是平行四边形即可．
解答 证明：∵BE=DF，
∴DE=BF，
∵AB⊥EF于B，CD⊥EF于D，
∴∠EDC=∠ABF，
在Rt△EDC和Rt△ABF中，
$\left\{\begin{array}{l}{EC=AF}\\{ED=BF}\end{array}\right.$，
∴△EDC≌△FBA，
∴∠DEC=∠AFB，
∴AF∥EC，
∵AF=EC，
∴四边形AECF是平行四边形，
∴AE=CF．
点评 本题考查全等三角形的判定和性质，平行四边形的判定和性质等知识，解题的关键是正确寻找全等三角形，学会利用平行四边形的性质证明线段相等，属于中考常考题型．
练习册系列答案
相关题目
如图所示，AB=DB，∠ABD=∠CBE，∠E=∠C，求证：DE=AC．
如图，在△ABC中，DE∥BC，△ABC的高AM交DE于点N，BC=15，AM=10，DE=MN，求MN的长．