题目内容
4.若用直径为20cm的圆,做成两个完全相同的圆锥形容器的侧面(材料无浪费,接缝不计),那么每个圆锥形容器的高为5$\sqrt{3}$cm.分析 设每个圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=$\frac{1}{2}$•2π10,解得r=5,然后利用勾股定理计算圆锥的高.
解答 解:设每个圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{1}{2}$•2π10,解得r=5,
所以每个圆锥的高=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$(cm).
故答案为$5\sqrt{3}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若△ABC的三个内角满足3∠A>5∠B,3∠C<2∠B,则三角形是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 都有可能 |
9.用配方法解一元二次方程x2+6x+7=0,则方程可化为( )
| A. | (x+3)2=9 | B. | (x-3)2=2 | C. | (x+3)2=2 | D. | (x-3)2=7 |
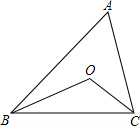 如图,在△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的角平分线,求:
如图,在△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的角平分线,求: 小强和小颖利用如图所示的两个转盘做游戏,同时转动A,B两个转盘,转盘停止转动后,若指针所指的数字之和为奇数,小强获胜;若指针所指的数字之和为偶数,则小颖获胜;若指针指在分界线上,重新转动两个转盘,这个游戏对双方公平吗?答:公平.
小强和小颖利用如图所示的两个转盘做游戏,同时转动A,B两个转盘,转盘停止转动后,若指针所指的数字之和为奇数,小强获胜;若指针所指的数字之和为偶数,则小颖获胜;若指针指在分界线上,重新转动两个转盘,这个游戏对双方公平吗?答:公平.