题目内容
1. 已知二次函数的解析式是y=x2-2x-3
已知二次函数的解析式是y=x2-2x-3(1)用配方法将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)在直角坐标系中,用五点法画出它的图象;
(3)利用图象求当x为何值时,函数值y<0
(4)当x为何值时,y随x的增大而减小?
(5)当-3<x<3时,观察图象直接写出函数值y的取值的范围.
分析 (1)利用配方法将函数解析式进行转换即可;
(2)根据顶点式求得顶点坐标,令x=0,求得与y轴的交点,令y=0,求得与x轴的坐标,再在对称轴的两侧取两组对称点,列表,然后描点、连线即可.
(3)、(4)、(5)根据二次函数图象的性质即可解答.
解答 解:(1)y=x2-2x-3=(x-1)2-4,即y=(x-1)2-4;
(2)由(1)可知,y=(x-1)2-4,则顶点坐标为(1,-4),
令x=0,则y=-3,
∴与y轴交点为(0,-3),
令y=0,则0=x2-2x-3,解得x1=-1,x2=3,
∴与x轴交点为(-1,0),(3,0).
列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y=x2-2x-3 | … | 0 | -3 | -4 | -3 | 0 | … |
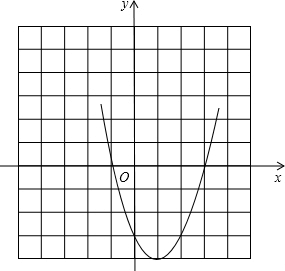
(3)由图象知,当-1<x<3时,函数值y<0;
(4)由图象知,当x<1时,y随x的增大而减小;
(5)当x=-3时,y=9+6-3=12,则-3<x<3时,0<y<12.
点评 本题考查了二次函数的图象,二次函数的性质,二次函数图象上点的坐标特征,找到顶点及对称轴,根据对称轴取点是画图的关键一步.

练习册系列答案
相关题目
16.用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )
| A. | 棱柱 | B. | 圆柱 | C. | 圆锥 | D. | 棱锥 |
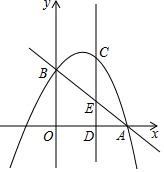 如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E.
如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E.