题目内容
10.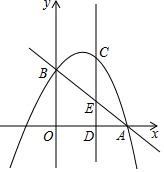 如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E.
如图,直线y=-x+2与x轴、y轴分别相交于A、B两点,抛物线y=-x2+bx+c经过点A和点B,C是第一象限内抛物线上的一动点,过点C作CD⊥x轴于点D,交直线AB于点E.(1)求抛物线的解析式;
(2)求线段CE长度的最大值;
(3)当线段CE长度最大时,射线DC上是否存在点F,使△ABF为等腰三角形,若存在,求出点F的坐标,若不存在,说明理由.
分析 (1)先求得点A和点B的坐标,然后将点A、B的坐标代入抛物线的解析式求得b、c的值,从而可求得抛物线的解析式;
(2)设点C的坐标为(x,-x2+x+2)、则点E的坐标为(x,-x+2),从而可列出CE的长度的代数式,然后依据配方法可求得CE的最大值;
(3)设点F的坐标为(1,a),然后依据两点间的距离公式列出关于a的方程求解即可.
解答 解:(1)∵将x=0代入y=-x+2得:y=2,
∴B(0,2).
∵将y=0代入y=-x+2得:-x+2=0,解得:x=2,
∴A(2,0).
将点A、B的坐标代入得:$\left\{\begin{array}{l}{c=2}\\{-4+2b+2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$.
∴抛物线的解析式为y=-x2+x+2.
(2)设点C的坐标为(x,-x2+x+2)、则点E的坐标为(x,-x+2)则CE=-x2+x+2-(-x+2)=-(x-1)2+1.
当x=1时,EC有最大值,最大值为1.
(3)设点F的坐标为(1,a).
①当FB=FA时,由两点间的距离公式可知:12+(a-2)2=12+a2.
解得a=1.
∴点F的坐标为(1,1).
∴点F与点E重合,不能构成三角形.
②当FB=BA时,由两点间的距离公式可知:12+(a-2)2=22+22.
解得a=2+$\sqrt{7}$或a=2-$\sqrt{7}$(舍去).
∴点F的坐标为(1,2+$\sqrt{7}$).
③当AF=AB时,由两点间的距离公式可知:12+a2=22+22.
解得:a=$\sqrt{7}$或a=-$\sqrt{7}$(舍去).
∴点F的坐标为(1,$\sqrt{7}$).
综上所述,点F的坐标为(1,2+$\sqrt{7}$)或(1,$\sqrt{7}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,配方法求二次函数的最值,依据两点间的距离公式,依据两点间的距离公式列出关于a的方程是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | 2x+3y=4xy | B. | 10y2-5y2=5 | C. | 2y+4y=6y2 | D. | 12x-2x=10x |
 已知二次函数的解析式是y=x2-2x-3
已知二次函数的解析式是y=x2-2x-3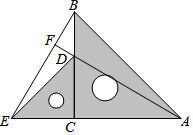 把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.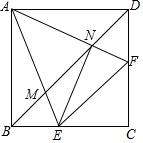 如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN
如图,四边形ABCD是正方形,点E和点F分别在BC和CD上,∠EAF=45°,AE、AF分别交BD于点M、N,连接EF,EN