题目内容
 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的同侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的同侧,AB=24cm,CD=10cm,求AB和CD的距离.考点:垂径定理,勾股定理
专题:
分析:过O作OF⊥CD于F,交AB于E,连接OA、OC,根据垂径定理求出AE=BE=
AB=12cm,CF=DF=
CD=5cm,在Rt△OEA和Rt△OFC中由勾股定理求出OE和OF即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:过O作OF⊥CD于F,交AB于E,连接OA、OC,
∵AB∥CD,
∴OF⊥AB,
∵OF过O,AB=24cm,CD=10cm,
∴AE=BE=
AB=12cm,CF=DF=
CD=5cm,
在Rt△OEA中,OA=13cm,由勾股定理得:OE=
=
=5(cm),
在Rt△OFC中,OC=13cm,由勾股定理得:OF=
=
=12(cm),
∴EF=OF-OE=7cm,
即AB和CD的距离是7cm.

解:过O作OF⊥CD于F,交AB于E,连接OA、OC,
∵AB∥CD,
∴OF⊥AB,
∵OF过O,AB=24cm,CD=10cm,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OEA中,OA=13cm,由勾股定理得:OE=
| OA2-AE2 |
| 132-122 |
在Rt△OFC中,OC=13cm,由勾股定理得:OF=
| OC2-CF2 |
| 132-52 |
∴EF=OF-OE=7cm,
即AB和CD的距离是7cm.
点评:本题考查了勾股定理,垂径定理的应用,解此题的关键是构造直角三角形,题目比较好,难度适中.

练习册系列答案
相关题目
在代数式:a,
(a+b)h,3.14k2,
,
,
,中,单项式的个数为( )
| 1 |
| 2 |
| 1 |
| a |
| 3x-1 |
| 2 |
| 1 |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知
如图,已知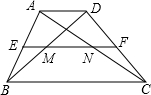 如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.
如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.