题目内容
9. 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为a,则sina的值为$\frac{4}{5}$.
如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为a,则sina的值为$\frac{4}{5}$.
分析 作PH⊥x轴于H,如图,利用P点坐标得到OH=3,PH=4,则根据勾股定理可计算出OP,然后根据正弦的定义求解.
解答 解:作PH⊥x轴于H,如图,
∵P点坐标为(3,4),
∴OH=3,PH=4,
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴sinα=$\frac{PH}{OH}$=$\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.熟练掌握勾股定理和锐角三角函数的定义.

练习册系列答案
相关题目
18.在△ABC中,AB=6,AC=8,BC=11,则该三角形为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
19. 如图,把一张长方形纸片ABCD沿EF折叠,若∠1=40°,则∠AEF的度数为( )
如图,把一张长方形纸片ABCD沿EF折叠,若∠1=40°,则∠AEF的度数为( )
 如图,把一张长方形纸片ABCD沿EF折叠,若∠1=40°,则∠AEF的度数为( )
如图,把一张长方形纸片ABCD沿EF折叠,若∠1=40°,则∠AEF的度数为( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
 如图是统计学生跳绳情况的频数分布直方图,如果跳 75次以上(含75次)为达标,则达标学生所占比例为90%.
如图是统计学生跳绳情况的频数分布直方图,如果跳 75次以上(含75次)为达标,则达标学生所占比例为90%.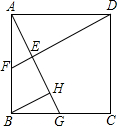 如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?