题目内容
4.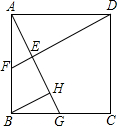 如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?
分析 利用正方形的性质和条件可证明△AED≌△BHA,可求得AH=DE,再利用线段的和差关系可求得结论.
解答 解:AG=DE+HG.
证明如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,AB∥CD,
∴∠ABH=∠CDE=∠AFE,
∴DF∥BH,
∵DE⊥AG,
∴∠BHA=∠AED=90°,
∴∠BAH+∠DAE=∠DAE+∠ADE,
∴∠BAH=∠ADE,
在△AED和△BHA中
$\left\{\begin{array}{l}{∠ADE=∠BAH}\\{∠AED=∠BHA}\\{AD=AB}\end{array}\right.$
∴△AED≌△BHA(AAS),
∴DE=AH,
∵AG=AH+HG,
∴AG=DE+HG.
点评 本题主要考查正方形的性质和全等三角形的性质,由条件证得△AED≌△BHA是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为a,则sina的值为$\frac{4}{5}$.
如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为a,则sina的值为$\frac{4}{5}$.