题目内容
9．
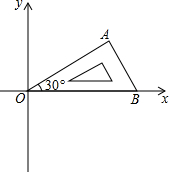将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中，OB在x轴上，若OA=4，将三角板绕原点O逆时针旋转，每秒旋转60°，则第2017秒时，点A的对应点A′的坐标为（ ）| A． | （0，4） | B． | （2$\sqrt{3}$，-2） | C． | （-2$\sqrt{3}$，2） | D． | （0，-4） |
分析 根据OA的长度结合旋转的性质即可得出第1秒时，点A的对应点A′的坐标为（0，4），再由三角板每秒旋转60°，可得出点A′的位置6秒一循环，由此即可得出第2017秒时，点A的对应点A′的坐标与第一秒时相同，此题得解．
解答 解：∵OA=4，∠AOB=30°，将三角板绕原点O逆时针旋转，每秒旋转60°，
∴第1秒时，点A的对应点A′的坐标为（0，4）．
∵三角板每秒旋转60°，
∴点A′的位置6秒一循环．
∵2017=336×6+1，
∴第2017秒时，点A的对应点A′的坐标为（0，4）．
故选A．
点评 本题考查了坐标与图形的变化中的旋转以及规律型中点的坐标，根据每秒旋转的角度，找出点A′的位置6秒一循环是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
19．-$\frac{1}{5}$的倒数是（ ）
| A． | -5 | B． | 5 | C． | -$\frac{1}{5}$ | D． | $\frac{1}{5}$ |
17．下列说法不正确的是（ ）
| A． | 调查一架“歼20”隐形战机各零部件的质量，应采用抽样调查 | |
| B． | 一组数据2，2，3，3，3，4的众数是3 | |
| C． | 如果x1与x2的平均数是4，那么x1+1与x2+5的平均数是7 | |
| D． | 一组数据1，2，3，4，5的方差是2，那么数据11，12，13，14，15的方差也是2 |
过⊙O上任意一点B作过圆心O的直线交⊙O于另一点E，点A为BE延长线上任意一点，过点A作⊙O的切线AB，切点为点D，过B作BC⊥AD于C，BC交⊙O于点F，连BD
14．把二次根式$\sqrt{\frac{27}{2}}$化简成最简二次根式，结果为（ ）
| A． | 3$\sqrt{\frac{3}{2}}$ | B． | 9$\sqrt{\frac{1}{6}}$ | C． | $\frac{\sqrt{54}}{2}$ | D． | $\frac{3\sqrt{6}}{2}$ |
1．
数学小组的同学为了解“阅读经典”活动的开展情况，随机调查了50名同学，对他们一周的阅读时间进行了统计，并绘制成如图所示的条形统计图，这组数据的中位数和众数分别是（ ）
数学小组的同学为了解“阅读经典”活动的开展情况，随机调查了50名同学，对他们一周的阅读时间进行了统计，并绘制成如图所示的条形统计图，这组数据的中位数和众数分别是（ ）| A． | 中位数和众数都是8小时 | B． | 中位数是25人，众数是20人 | ||
| C． | 中位数是13人，众数是20人 | D． | 中位数是6小时，众数是8小时 |
19．
中国象棋是中华民族的文化瑰宝，它渊远流长，趣味浓厚．如图，在某平面直角坐标系中，
所在位置的坐标为（-3，1），
所在位置的坐标为（2，-1），那么，
所在位置的坐标为（ ）
中国象棋是中华民族的文化瑰宝，它渊远流长，趣味浓厚．如图，在某平面直角坐标系中，所在位置的坐标为（-3，1），所在位置的坐标为（2，-1），那么，所在位置的坐标为（ ）| A． | （0，1） | B． | （4，0） | C． | （-1，0） | D． | （0，-1） |