题目内容
11.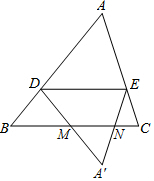 如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.(1)求证:DB=DM.
(2)若$\frac{AD}{DB}$=2,DE=6,求线段MN的长.
(3)若$\frac{AD}{DB}$=n(n≠1),DE=a,则线段MN的长为a-$\frac{a}{n}$(n>1)或$\frac{a}{n}$-a(0<n<1)(用含n的代数式表示).
分析 (1)根据翻折的性质以及平行线的性质即可求证∠B=∠DMB,从而可知DB=DM;
(2)根据相似三角形的判定求证△A′MN∽△A′DE,从而$\frac{MN}{DE}=\frac{A′M}{A′D}$=$\frac{1}{2}$,从可求出MN=$\frac{1}{2}$DE=3;
(3)由(2)可知:△A′MN∽△A′DE,利用相似三角形的性质即可求出MN的长度,由于n没有说明情况故需要进行分类讨论.
解答 解:(1)∵DE∥BC,
∴∠ADE=∠B,∠A′DE=∠DMB,
由翻折可知:∠ADE=∠A′DE
∵∠B=∠DMB,
∴DB=DM,
(2)由翻折可知:A′D=AD
∵$\frac{AD}{DB}=2$,DB=DM,
∴$\frac{A′D}{DM}=2$,
∴$\frac{A′M}{A′D}$=$\frac{1}{2}$
∵DE∥BC,
∴△A′MN∽△A′DE
∴$\frac{MN}{DE}=\frac{A′M}{A′D}$=$\frac{1}{2}$
∵DE=6,
∴MN=$\frac{1}{2}$DE=3,
(3)由翻折可知:A′D=AD
∵$\frac{AD}{DB}$=n,DB=DM,
∴$\frac{A′D}{DM}$=n,
当n>1时,
∴$\frac{A′M}{A′D}$=$\frac{n-1}{n}$
∵DE∥BC,
∴△A′MN∽△A′DE
∴$\frac{MN}{DE}=\frac{A′M}{A′D}$=$\frac{n-1}{n}$
∵DE=a,
∴MN=$\frac{n-1}{n}$DE=a-$\frac{a}{n}$,
同理:当0<n<1时,
此时∴$\frac{A′M}{A′D}$=$\frac{1-n}{n}$,
∴MN=$\frac{a}{n}-a$,
综上所述,MN=a-$\frac{a}{n}$(n>1)或$\frac{a}{n}$-a(0<n<1)
故答案为:(3)MN=a-$\frac{a}{n}$(n>1)或$\frac{a}{n}$-a(0<n<1)
点评 本题考查相似三角形的综合问题,解得关键是熟练运用相似三角形的性质与判定,本题属于中等题型.

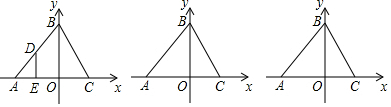
 在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.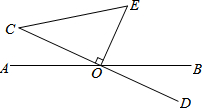 如图,AB,CD交于点O,OE⊥CD于O,连接CE,
如图,AB,CD交于点O,OE⊥CD于O,连接CE,